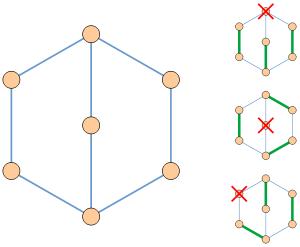
Un grafic critic, împreună cu cea mai mare potrivire a subgrafurilor obținute prin eliminarea unuia dintre vârfuri.
Grafic critic factor (sau grafic aproape sochetaemy.) - este un grafic cu n vârfuri, în care fiecare sub-cutii cu n - 1 are un perfect noduri de potrivire. (Potrivire perfectă în grafic. - un subset al marginilor cu proprietatea că fiecare dintre nodurile unui nod final de exact o margine a subsetul)
O combinație care acoperă toate vârfurile, cu excepția unuia, se numește o potrivire aproape perfectă. Astfel, în mod echivalent, un grafic critic este un grafic în care există potriviri aproape perfecte care nu conțin nici unul dintre vârfuri.
Trei grafice ale relațiilor prietenoase. Exemple de grafice non-hamiltonian-factor critice
Orice ciclu de lungime impare este factor critic. Ca orice grafic complet cu un număr impar de noduri. Mai general, orice grafic Hamiltonian cu un număr impar de vârfuri este critic factor. Graficele relațiilor prietenoase (graficele formate prin îmbinarea unui set de triunghiuri cu un vertex comun) oferă exemple de grafice, factor critice, dar nu Hamiltonian.
Dacă graficul G este factor critic, atunci este un Mouselian al lui G. De exemplu, graficul Grouch. Ciclul ciclic cu cinci vârfuri este factor critic.
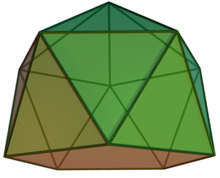
Orice grafic vertex 2 conectat fără gheare cu un număr impar de vârfuri este factor critic. De exemplu, un grafic cu noduri 11 noduri formate dintr-un icosaedru regulat (grafic răsucite piramide pentagonale alungite [en]), este ca 2-conectat și liber de gheara, astfel încât acesta este un factor critic. Acest rezultat rezultă direct din teorema mai fundamentală că orice grafic conectat fără gheare cu un număr par de vârfuri are o potrivire perfectă.
Graficele grafice grafice pot fi descrise în câteva moduri diferite, diferite de definiție ca grafice, eliminarea oricărui vârf care permite potrivirea perfectă:
- Tibor Gallai [en] a demonstrat că graficul este factor critic dacă și numai dacă este conectat și pentru orice vârf v al graficului, există cea mai mare potrivire. care nu include v. Din această proprietate rezultă că graficul trebuie să aibă un număr impar de vârfuri și că orice potrivire cea mai mare trebuie să includă un singur vârf.
- Laszlo Lovas a demonstrat că graficul este critic factor dacă și numai dacă are o descompunere a urechilor ciudate. coaste partițiilor de pe secvența de subgrafurilor fiecare dintre care este calea sau ciclul de lungime impar, iar primele sub-casetele din secvența este un ciclu, fiecare cale în secvența are o noduri interne finite dar nu pe subgrafurilor anterioare, și fiecare ciclu este diferit de primul, are exact un vertex comun subgrafelor anterioare. De exemplu, graficul din figură poate fi rupt în acest mod, cu cinci muchii cicluri și căi cu trei muchii. În cazul în care este, de asemenea, dat de potrivire aproape perfect grafic factor critic, descompunerea otic poate fi selectat astfel încât fiecare ureche se extinde în mod alternativ margini potrivite și marginile care nu sunt incluse în potrivire.
- Graf este, de asemenea, un factor critic dacă și numai dacă poate fi redus la un grafic cu un singur nod prin strângerea cicluri de lungime impar. Mai mult decât atât, în acest caz, este posibil să se aleagă fiecare ciclu în secvență, astfel încât acesta conține vârf rezultat contracția ciclului anterior. De exemplu, în cazul în care urechile de tragere ureche Descompunerea în ordinea specificată prin descompunere, de fiecare dată ureche contractabile formează un ciclu ciudat, astfel încât descrierea folosind o descompunere a urechii poate fi folosită pentru a căuta secvența de cicluri de ciudat contracție. In schimb, succesiunea contracțiilor cicluri impare conținând vârfuri obținute în contracțiile anterioare pot fi formate în expansiune a urechii, în care o multitudine de urechi formate margini contractabile.
- Să presupunem că graficul G este dat împreună cu vârful selectat v și M corespunzând cu toate nodurile, altele decât v. Atunci G este-factor critic dacă și numai dacă există mai multe moduri în G. constând în atingerea alternativ marginile corelări și coaste, care nu se potrivesc, care leagă vârful v la toate celelalte noduri ale lui G. Bazat pe această proprietate, puteți defini pentru timp liniar. este graficul G cu un coeficient critic de potrivire aproape perfect.
Graficele cu factor critic trebuie să aibă întotdeauna un număr impar de vârfuri și trebuie să fie marginile 2 legate (adică nu pot avea niciun pod). Cu toate acestea, acestea nu sunt neapărat legate de vertex 2. Graficele relațiilor prietenoase oferă un exemplu. Graficul grafic critic nu poate fi bipartit. deoarece într-un grafic bipartit cu o potrivire aproape perfectă numai vârfurile care pot fi îndepărtate pentru a obține un grafic cu potrivire perfectă se află pe partea mai mare a graficului bipartit.
Orice nod 2-un grafic conectat coeficient critic cu m nervuri are cel puțin m diferite corelările aproape perfectă și, mai general, orice grafic factor critic cu m muchii și unități c (componentele conectate cu 2 vârfuri) are cel puțin m - c + 1 diferite potriviri aproape perfecte. Graficele pentru care aceste limite sunt exacte pot fi descrise ca având o extindere a urechii unui anumit tip.
Orice grafic conectat poate fi transformat într-un grafic critic factor prin contractarea unor margini suficient de multe. Setul minim de margini care trebuie contractat pentru a face graficul critic G dat reprezintă o bază pentru matroid. din care rezultă că un algoritm lacomi care lucrează pentru timpul polinomial poate fi folosit pentru a găsi cel mai mic set de margini ponderate, contracția cărora face ca graficul să fie critic. Cel mai vechi algoritm pentru contractarea unui număr minim de margini (neimpozitate) pentru a obține un grafic critic pentru factori poate fi găsit în articolul lui Frank.
O floare este un subgraf critic al unui grafic mai mare. Flori joacă un rol-cheie în algoritmii [en] Edmonds [en] Căutare de potrivire maximă și minimă combinație perfectă ponderată în graficul non-bipartit.
În combinatoriile polyhedra, graficele critice în funcție de cote joacă un rol important în descrierea fațetelor de polyhedra ale combinațiilor potrivite ale unui grafic dat.
Generalizări și concepte conexe
Se spune că factorul k este critic dacă orice subset al n-k vertices are o potrivire perfectă. Cu această definiție, un grafic aproape compatibil (en: hypomatchable) este critic de 1 factor. Chiar mai general, un grafic (a, b)--factor critică dacă orice subset al n - k noduri este r-factor, adică este un set de noduri-r regulate ale subgrafic Graficul dat.
Când se vorbește despre un grafic critic (fără a se specifica k-), de obicei se înțelege un graf, eliminarea oricărui vârf conduce la o scădere a numărului de culori necesare pentru colorarea graficului. Conceptul criticității este folosit mult mai larg în teoria graficelor pentru grafice, în care eliminarea oricărui vârf modifică unele proprietăți ale graficului. Critic prin combinații de grafice este un grafic pentru care eliminarea oricărui vârf nu modifică dimensiunea celei mai mari potriviri. Potrivit lui Galla, graficele care sunt critice în combinații sunt exact grafice în care orice componentă conectată este factor critic. Adăugarea graficului critic este în mod necesar critică în combinații, faptul că Gallai a folosit pentru a dovedi limita inferioară a numărului de vârfuri ale graficului critic.
În afara teoriei grafurilor, noțiunea de factor-criticitate are o extindere la matroizi prin determinarea tipului de descompunere a urechii la matroizi. Un matroid este un factor critic dacă are o decădere a urechii, în care toate urechile sunt ciudate.