Nevoia de a rezolva ecuații nu numai din primul, dar și al celui de-al doilea grad din antichitate, a fost cauzată de necesitatea de a rezolva problemele legate de găsirea zonelor terestre și a lucrărilor de terasament de natură militară, precum și de dezvoltarea astronomiei și a matematicii în sine.
O ecuație a formei ax 2 + bx + c = 0, unde a. b. c - numere reale, unde a ≠ 0, se numește ecuație patratică.
Dacă a = 1. atunci ecuația patratică este numită redusă; dacă o ≠ 1, atunci nereducătoare.
Numerele a. b. c au urmatoarele nume: a - primul coeficient, b - al doilea coeficient, c - termenul liber.
Rădăcinile ecuației axei 2 + bx + c = 0 sunt găsite prin formula
Expresia D = b 2 - 4ac este numită discriminant al ecuației patratice.
- dacă D <0, то уравнение не имеет действительных корней;
- dacă D = 0, atunci ecuația are o rădăcină reală;
- dacă D> 0, atunci ecuația are două rădăcini reale.
În cazul în care D = 0, uneori se spune că ecuația cuadratoare are două rădăcini identice.
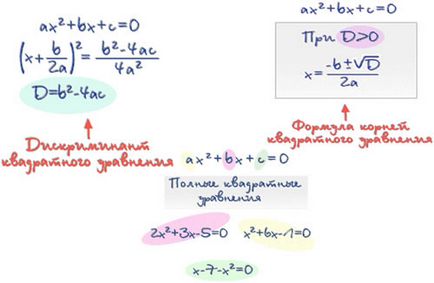
Ecuația cuadratoare totală
Ecuații parțiale eșalonate
Dacă în ecuația patratică axa 2 + bx + c = 0 al doilea coeficient b sau termenul liber c este zero, atunci ecuația patratică este numită incompletă.
Ecuațiile incomplete se disting prin faptul că pentru a-și găsi rădăcinile este posibil să nu se folosească formula rădăcinilor unei ecuații patrate - este mai simplu să se rezolve ecuația prin descompunerea părții stângi în multiplicatori.
Metode de rezolvare a ecuațiilor patrate incomplete:
Soluția ecuației quadrate incomplete
Ecuații pătrate cu variabile complexe
Mai întâi considerăm cea mai simplă ecuație cuadratoare z 2 = a. unde a este un număr dat și z este un număr necunoscut. Pe setul de numere reale această ecuație:
- are o rădăcină z = 0 dacă a = 0;
- are două rădăcini reale z1, 2 = ± √a
- Nu are rădăcini reale dacă a <0
Rezolvarea ecuatiilor patrate folosind grafice
Fără a folosi formula, ecuația patratică poate fi rezolvată grafic. De exemplu, x 2 + x + 1 = 0.
Rezolvăm ecuația. Pentru aceasta vom construi două grafice y = x 2; y = x + 1.
y = x 2. funcția patratică, graficul parabolei.
y = x + 1, o funcție liniară, graficul este o linie dreaptă.
Graficele se intersectează la două puncte, ecuația are două rădăcini.
Răspuns: x ≈ -0,6; x ≈ 2.6.
Rezolvarea problemelor folosind ecuații patrate