Din Wikisource
segmente din lemn (Engl Segment de copac.) - o structură de date care permite asimptotică să pună în aplicare orice operațiuni definite de setul pe care operațiunea este asociativă, și există un element neutru în ceea ce privește funcționarea, care este, monoid. De exemplu, însumarea mulțimea numerelor naturale, căuta orice set minim număr, matrice de multiplicare pe set de matrice, set de liste uniune cel mai mare divizor comun al setului de numere întregi și polinoame.
În acest caz, este posibilă, de asemenea, modificarea elementelor matricei: atât schimbarea valorii unui element, cât și schimbarea elementelor din întregul subsegment al matricei. de exemplu, puteți atribui o valoare tuturor elementelor sau puteți adăuga un număr la toate elementele matricei. Structura ocupă memoria, iar construcția acesteia necesită timp.
[edit] Structura
Structura este un arbore, frunzele cărora sunt elemente ale matricei originale. Alte vârfuri din acest arbore au doi copii și conțin rezultatul operației de la copiii lor (de exemplu, un minim sau o sumă). Astfel, rădăcina conține rezultatul funcției dorite din întreaga matrice, copilul stâng al rădăcinii conține rezultatul funcției pe, iar rezultatul, respectiv, rezultatul. Și așa mai departe, trecând mai adânc în copac.
[edit] Construirea unui copac
Fie matricea originală constând din elemente. Pentru comoditatea construirii, mărim lungimea matricei astfel încât să fie egală cu cea mai apropiată putere de două; , unde. Aceasta se face pentru a împiedica accesul la elementele inexistente ale matricei în timpul procesului de construcție ulterioară. Elementele goale trebuie să fie umplute cu elemente neutre ale monoidului. Apoi, pentru a stoca arborele de segmente, avem nevoie de o serie de elemente, deoarece în cel mai rău caz, numărul de vârfuri din arbore poate fi estimat de suma, unde. Astfel, structura ocupă memorie liniară.
Procesul de construire a unui copac este de a umple matricea. Se umple matrice, astfel încât elementul i-lea ar fi rezultatul unei operații binare (pentru fiecare dintre sale specifice sarcinii) numerele elementelor și c, adică părintele a fost rezultatul unei operații binare de fii. O opțiune este să o faceți recursiv. Să presupunem că avem o serie de surse, precum și variabile care indică frontiera intervalului curent. Vom începe procedura construirii segmentelor rădăcină copac (,,), precum și construcția procedurii în sine, în cazul în care nu este cauzată de o foaie de sine apeluri de la fiecare dintre cei doi fii și însumează valorile calculate, iar în cazul în care este cauzată de foaia - este pur și simplu scrie o valoare de element al matricei (Pentru aceasta avem matricea originală). Asimptotica construirii unui copac al segmentelor este prin urmare.
Există două modalități principale de a construi un copac al segmentelor: construcția de dedesubt și construcția de deasupra. În construirea algoritmul de jos se ridica din frunze la rădăcină (doar începe să umple elementele de matrice de index mai mare pentru mai puțin atunci când se completează elemente ale copiilor săi, și va fi completat deja, și putem calcula cu ușurință operația binară pe ele), precum și în construcția de sus în jos de rădăcină la frunze. Modificări speciale apar în implementarea interogărilor pentru astfel de segmente de copaci.
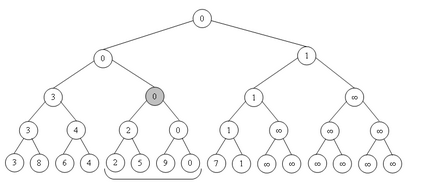
Implementarea construcției de sus:
Implementarea construcției de jos: