Nu-mi amintesc când am învățat prima dată despre topologie, dar această știință ma interesat imediat. Ceainicul se transformă într-un geam, sfera este întoarsă spre interior. Mulți au auzit despre asta. Dar cei care doresc să pătrundă în acest subiect la un nivel mai grav, au adesea dificultăți. Mai ales acest lucru se aplică la stăpânirea celor mai elementare concepte, care sunt în mod inerent foarte abstracte. Mai mult, multe surse par să intenționeze în mod specific să confunde cititorul. Să presupunem că un wiki rus oferă o declarație foarte vagă despre ceea ce face topologia. Se spune că aceasta este o știință care studiază spații topologice. În articolul despre spațiile topologice, cititorul poate învăța că spațiile topologice sunt spații echipate cu topologie. Asemenea explicații în stilul sepulilor lui Lemov nu clarifică esența subiectului. Voi încerca să subliniez în continuare conceptele de bază într-o formă mai clară. În nota mea nu vor mai exista cazane și covrigi, dar primii pași vor fi luați, ceea ce va învăța în cele din urmă această magie.
Totuși, din moment ce nu sunt un matematician, ci o umanistă sută la sută, este posibil ca ceea ce este scris mai jos să fie minciuni! Ei bine, sau cel puțin o parte din ea.
Începem cu o scurtă repetare a teoriei seturilor. Cred că majoritatea cititorilor sunt familiarizați cu ea, dar totuși îți voi aminti elementele de bază.
Deci, se crede că setul nu are definiții și că înțelegem intuitiv ce este. Cantor a spus: "Prin" set "se înțelege o legătură într-un întreg întreg M de anumite obiecte distincte ale contemplației noastre sau ale gândirii noastre (care se vor numi" elemente "ale mulțimii M). Desigur, aceasta este doar o descriere alegorică, nu o definiție matematică.
Teoria seturilor este cunoscută (îmi cer scuze pentru joc) cu multe paradoxuri uimitoare. De exemplu. Criza matematicii la începutul secolului al XX-lea este, de asemenea, asociată cu aceasta.
Seturile sunt finite.

Sunt fără sfârșit. De exemplu, setul de numere întregi, care este notat cu litera ℤ (sau pur și simplu Z, dacă nu aveți litere brute pe tastatură).

În cele din urmă, există un set gol. Este exact una din întregul univers. Există o simplă dovadă a acestui fapt, dar nu o voi da aici.

Dacă setul este infinit, acesta este numărabil. Countable - acele seturi ale căror elemente pot fi renumerotate prin numere naturale. Setul de numere naturale, așa cum ați ghicit, este, de asemenea, numărare. Dar cum puteți număra numerele întregi.
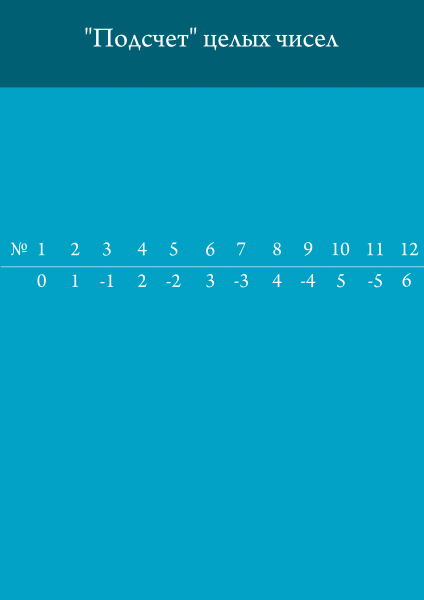
Cu numere raționale, este mult mai complicat, dar este, de asemenea, susceptibil la numerotare. Această metodă se numește proces diagonal și arată ca imaginea de mai jos.
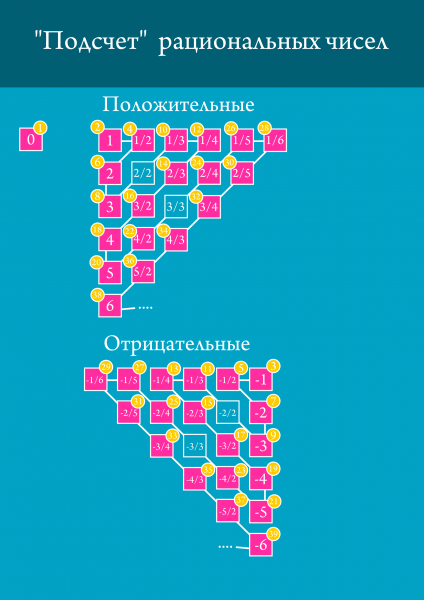
Vom muta zig-zag pe numere raționale, începând cu 1. În acest caz, pentru fiecare număr pe care îl obținem, îi atribuim un număr par. Numerele raționale negative sunt tratate în același mod, numai numerele sunt ciudate, începând de la 3. Zero primește în mod tradițional primul număr. Astfel, este clar că toate numerele raționale pot fi numerotate. Toate numerele, cum ar fi 4,87592692976340586068 sau 1,00000000000001, sau -9092, sau chiar 42 își obțin numărul în acest tabel. Cu toate acestea, nu toate numerele cad aici. De exemplu, √2 nu primește un număr. Odată ce a fost foarte supărător pentru greci. Ei spun că tipul care a deschis numere iraționale sa înecat.
O generalizare a noțiunii de dimensiune pentru seturi este puterea. Puterea seturilor finite este egală cu numărul elementelor lor. Puterea seturilor infinite este marcată de litera alefului ebraic cu indexul. Cea mai mică putere infinită este puterea lui 0. Este egal cu puterea seturilor numărabile. După cum vedem, în acest fel, numerele naturale sunt la fel de multe ca întregi sau raționale. Ciudat, dar adevărat. Următoarea este puterea continuumului. Este notat cu þ1. Aceasta este cardinalitatea setului de numere reale ℝ, de exemplu. Există o ipoteză că puterea continuumului și puterea lui Aleph sunt una și aceeași. Ie că nu există o putere intermediară între seturile numărate și continuu.
Pe seturi, puteți efectua diverse operații și puteți obține seturi noi.
1. Seturile pot fi combinate.

2. Seturile pot fi "scăzute". Această operație se numește completare.

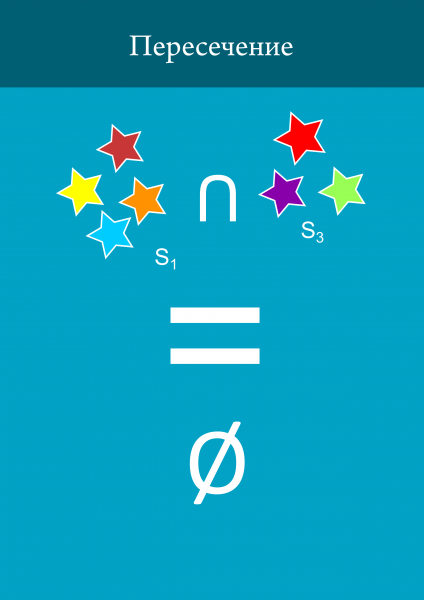
3. Se poate căuta intersecția seturilor.
De fapt, totul se referă la seturile pe care trebuie să le cunoașteți pentru scopurile acestui articol. Acum putem trece la foarte topologia.
Topologia este o știință care studiază seturi cu o anumită structură. Această structură este, de asemenea, numită topologie.
Să presupunem că avem un anumit set non-gol S.
Fie acest set o structură, care este descrisă cu ajutorul unui set, pe care îl vom numi T. T este setul de subseturi ale mulțimii S astfel încât:
1. S și Sam le aparțin T.
2. Orice unire a familiilor arbitrare ale elementelor lui T aparține lui T.
3. Intersecția unei familii arbitrare de elemente finite din T aparține lui T.
Dacă aceste trei elemente sunt satisfăcute, atunci structura noastră este topologia lui T pe mulțimea S. Elementele setului T sunt numite seturi deschise pe S în topologia lui T. Completarea seturilor deschise este seturile închise. Este important să rețineți că, dacă setul este deschis, acest lucru nu înseamnă că acesta nu este închis și invers. Mai mult decât atât, într-un set dat cu privire la o anumită topologie pot exista subseturi care nu sunt nici deschise, nici închise.
Să dăm un exemplu. Să presupunem că avem un set format din trei triunghiuri colorate.

Cea mai simplă topologie pe aceasta se numește topologia antidiscret. Aici este.

Această topologie este denumită și topologia punctelor blocate. Se compune din setul însuși și un set gol. Acest lucru într-adevăr satisface axiomele topologiei.
Topologiile multiple pot fi definite pe un singur set. Aici este o altă topologie foarte primitivă care se întâmplă. Se numește discret. Aceasta este o topologie care constă în toate subseturile unui set dat.

Iată o altă topologie. Acesta este dat pe un set de 7 stele multi-colorate S, pe care le-am notat cu litere. Asigurați-vă că este o topologie. Nu sunt sigur, am pierdut brusc un fel de unificare sau trecere. În această imagine trebuie să existe un set S însuși, un set gol, intersecții și uniuni ale tuturor celorlalte elemente ale topologiei trebuie, de asemenea, să fie în imagine.

O pereche de topologie și setul pe care este dat se numește un spațiu topologic.
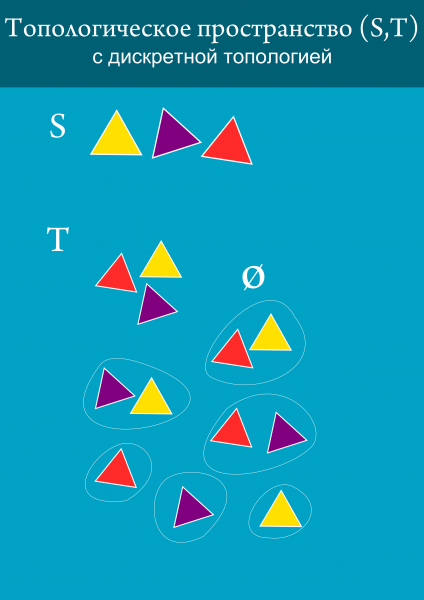
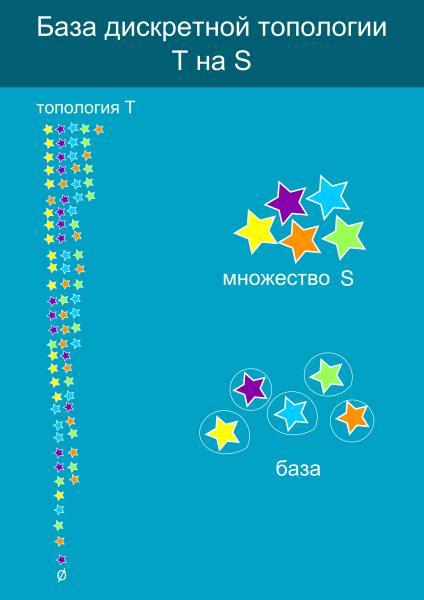
Dacă există mai multe puncte în set (ca să nu mai vorbim de faptul că pot fi infinit multe dintre ele), listarea tuturor seturilor deschise poate fi problematică. De exemplu, pentru o topologie discretă pe un set de trei elemente, trebuie să compilam o listă cu 8 seturi. Și pentru un set de 4 elemente, topologia discretă va consta în 16, pentru 5 - 32, pentru 6 - 64 și așa mai departe. Pentru a nu enumera toate seturile deschise, înregistrarea abreviată este folosită ca și cum ar fi pentru a scrie acele elemente ale căror uniuni pot da toate seturile deschise. Aceasta se numește baza topologiei. De exemplu, pentru o topologie discretă a unui spațiu de trei triunghiuri, vor fi luate trei triunghiuri separat, deoarece prin combinarea lor se pot obține toate celelalte seturi deschise în topologia dată. Ei spun că baza de date generează o topologie. Seturile ale căror elemente generează baza se numesc prebase.
Mai jos este un exemplu de bază de date pentru o topologie discretă pe un set de cinci stele. După cum puteți vedea, în acest caz baza de date constă doar din cinci elemente, în timp ce în topologia a 32 de subseturi. Sunt de acord, folosiți baza de date pentru a descrie topologia - mult mai convenabilă.
De ce avem nevoie de seturi deschise? Într-un sens, ei dau o idee despre "apropierea" dintre puncte și diferența dintre ele. Dacă punctele aparțin două seturi deschise diferite sau dacă un punct este într-un set deschis în care nu există un al doilea, atunci acestea sunt topologic diferite. Într-o topologie antidisectivă, toate punctele în acest sens nu pot fi diferențiate, par a fi blocate împreună. În schimb, într-o topologie discretă, toate punctele au o diferență.

Relația dintre un set deschis și o închidere poate fi formulată după cum urmează. Un set deschis este un set, fiecare element al căruia are o anumită vecinătate. Sau invers, putem spune că setul este deschis dacă este un cartier al oricăruia dintre punctele sale.
Toate acestea reprezintă noțiunea fundamentală de topologie. Prin urmare, nu este încă clar cum să întoarcem sferele spre interior. Poate în viitor, pot ajunge la un astfel de subiect (dacă mă gândesc singur).