
Acasă | Despre noi | feedback-ul
Cele mai importante exemple de mișcare a particulelor în puturile potențiale sunt mișcarea nucleonilor din nuclei, electronii din atomi și molecule. Legile de bază ale mișcării particulelor finite poate fi testată, de exemplu, atunci când forma potențialului reliefului ia forma dreptunghiulara infinit adincime de lățime a. În intervalul (0, a), energia potențială este presupus egal cu zero, și merge la infinit (Fig. 2.1) este în afara acestui interval. Ca rezultat, particula in miscare sa nu poate merge dincolo de limitele segmentului (0, a) sau, cum se spune, particula este într-un puț de potențial infinit profund de lățime a.
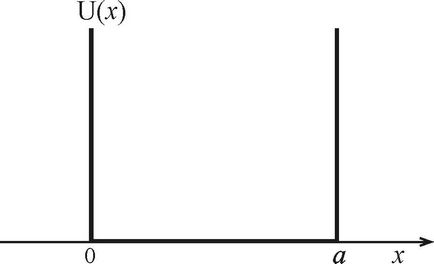
Fig. 2.1. Dreapta dreptunghiulară de profunzime infinită
Deoarece probabilitatea de a găsi o particulă în afara unei puțuri de potențial infinit de adâncime este zero, funcția de undă în afara intervalului (0, a) este zero. Astfel, obținem condițiile limită pentru soluția ecuației lui Schrödinger:
Deoarece energia potențială U (x) este independentă de timp, pentru a calcula funcțiile de undă a particulelor este necesară pentru a rezolva ecuația one-dimensional staționar Schrodinger cu potențial zero la fundul gropii. și anume
Reducem ecuația (2) în forma canonică:
este o cantitate cu dimensiunea valului: m - 1. Ecuația caracteristică: are rădăcini complexe. Soluția generală a ecuației diferențiale (3) poate fi scrisă în formular
Etapa staționară Schrödinger, așa cum este binecunoscută, conține un oscilator cu oscilare în timp cu frecvență
. ()
Primul termen reprezintă valul "care se încadrează" de Broglie cu amplitudinea A. Numărul și frecvența undelor. Al doilea termen este valul "reflectat" de Broglie, adică un val propagand în direcția opusă. Aceste valuri sunt coerente, deoarece au aceeași lungime de undă. De obicei, undele Broglie sunt înregistrate fără un multiplicator de timp, adică în forma (5).
Înlocuirea soluției de (5) în condiția limită. Avem și Aplicăm formula Euler. avem
unde este factorul de normalizare, care este calculat din condiția de normalizare. Înlocuind (6) condiția de normalizare
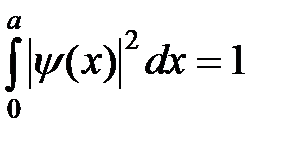
Acum înlocuim soluția (6) în cea de-a doua condiție limită: și ajungem acolo. unde n are o serie naturală de numere. Astfel, numărul de valuri k este cuantificat, adică are o serie de sensuri discrete
Substituind (7) în (6) avem în cele din urmă pentru funcțiile de undă care descriu starea particulei într-un puț de potențial infinit de adâncime de lățime a:
Pentru a obține spectrul energetic al particulei, înlocuim valorile numerelor de unde (7) găsite în formula (4):
După cum se vede, soluția (8) este un val permanent de Broglie, care a fost format ca urmare a interferenței „cădere“ și „reflectat“ coerent de valuri Broglie, definite prin relația (5) sau (). Condiția pentru formarea unui val de picioare (7) poate fi scrisă în ceea ce privește lungimea de undă de Broglie considerând că. atunci ajungem
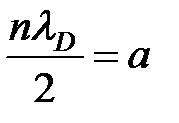
și anume se formează un val în picioare cu condiția ca un număr întreg de lungimi de jumătate de undă egal cu numărul cuantic n să fie așezat pe lățimea godeului. Densitatea de probabilitate, adică Probabilitatea de a detecta o particulă pe un interval de unitate al puțului este egală cu
În Fig. 2.2 prezintă funcțiile de undă ale particulei și densitatea de probabilitate corespunzătoare a primelor stări la n = 1,2,3 și la n = 20 >> 1.
Este evident că, la numere cuantice mici, distribuția de probabilitate pentru particula in put este puternic non-linear, dar cu o creștere a cuantumului funcției de densitate de probabilitate tinde să fie mai uniformă în limita numerelor cuantice mari. care corespunde trecerii la problema clasică. Într-adevăr, pentru numerele cuantice mari n >> 1, lungimea de undă a particulei devine mult mai mică decât lățimea puțului <<а. что соответствует условию применимости классического описания, в котором волновые свойства частицы не учитываются. В тоже время квантовомеханическое описание используется в случае соизмеримости длины волны де Бройля частицы и характерного размера системы, ограничивающего движение частицы (ширины ямы), что соответствует случаю малых квантовых чисел.
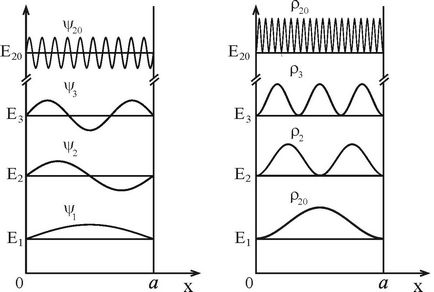
Fig. 2.2. Spectrul de energie, funcțiile de undă (a) și distribuția densității de probabilitate (b) a unei particule într-un puț de potențial dreptunghiular profund