
În acest post vom discuta despre aplicarea unei metode congruential liniară pentru o adâncime de biți număr pseudo-aleatoare de 64 de biți, și 128, explicând principiul de funcționare și de selecție a parametrilor.
Dacă întâmpinați dificultăți în folosirea unui RNG dintr-o bibliotecă standard, aveți cerințe nestandardiste față de acesta sau pur și simplu doriți să păstrați întregul proces de generare a numerelor aleatorii în aplicația dvs. sub control, bine ați venit la pisică.
Jos cu generatorul standard!
Toate limbile de programare destul de comune au funcții pentru a genera numere aleatorii (sau, pentru a fi extrem de precise, pseudorandom). Cu toate acestea, uneori devine necesară implementarea propriului generator de numere aleatoare (RNG). Deși RNG-ul este de obicei suficient de bun pentru a fi utilizat în majoritatea cazurilor, se întâmplă de asemenea că un generator prea abrupt pare să fie inutil, dar RNG-ul încorporat încă nu-i place.
Motivele pot fi diferite și nu sunt evidente la prima vedere. În primul rând, este demn de remarcat faptul că problema generării de numere aleatorii implică adesea găsirea unui echilibru între viteza muncii și calitatea rezultatului. Uneori trebuie să faceți ceva mai repede sau puțin mai greu.
În al doilea rând, RNG - nu doar o mizerie de operații aritmetice, și algoritm strict determinist, caracteristicile care pot varia foarte mult. În unele experimente științifice este necesar să se descrie complet condițiile de testare pentru a se asigura că acestea pot fi reproduse. Aceasta include algoritmul și parametrii RNG. În acest caz, este mai bine să aveți propria implementare.
Este posibil să apară o problemă în care este necesară operarea simultană a diferitelor RNG-uri. Este diferit, iar generatorul încorporat este de obicei unul. Desigur, puteți rula mai multe copii cu boabe inițiale diferite, dar în acest caz generatoarele vor produce elemente ale aceleiași secvențe (care se repetă ciclic), pornind de la diferite locuri. Durata ciclului este mare, dar teoretic acest lucru poate crea probleme.
În cazul meu, a fost necesar să se genereze numere de 128 biți. În C ++, nu există nici o funcție care să returneze cel puțin 64 de biți. După o călătorie lungă, am găsit confuzii în rand () și RAND_MAX în compilatoare diferite, un set de cârje pentru a genera 64 de biți și am decis să abandonez RNG-ul încorporat. Scrierea generatorului mi sa părut o sarcină elementară - pentru câteva iterații ale unui generator congruențial liniar, obțineți două numere pe 64 de biți și apoi le lipiți împreună. Nu a fost așa de simplu. Dar despre totul în ordine.
Deci, să începem să creăm un RNG. Ca bază, să luăm o metodă simplă și populară congruențială liniară care funcționează după formula:
unde xi. xi + 1 - numere aleatoare curente și următoare; a. c și m sunt câteva constante; mod este operatorul de a găsi restul diviziei.
Constanta m este adesea luată egală cu 2 32 sau 2 64 pentru a evita împărțirea în implementarea programului. Care au fost obținute ca urmare a unor resturi de 64 de biți, am folosit m = 2 64. Dar unde obținem o constantă, și c. În Wikipedia, următoarea pereche a fost găsit: a = c = 6364136223846793005 și 1442695040888963407. Fără să mă gândesc de două ori, am scris un generator folosind acești parametri și am început să testez algoritmul meu genetic. Cu toate acestea, el a devenit rapid obsedat. Suspiciunile au căzut pe RNG. Se pare că mai multe LSB în secvența obținută de pe 64 de biți numere „aleatoare“ nu demonstrează un comportament aleatoriu. Valorile unor biți de numere consecutive sunt afișate ca imagini monocrome:


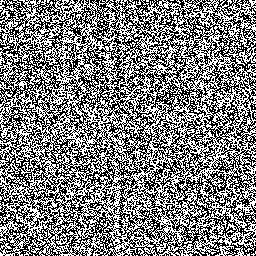
Valorile cifrelor 5, 15 și 20 inferioare (numerotate de la zero)
Aproximativ 20-24 de juniori nu sunt potriviți pentru utilizare. Odată cu creșterea numărului de descărcări, crește gradul de întâmpinare. Astfel, pentru a obține un număr aleatoriu de 64 biți, sunt necesare două iterații ale unui generator liniar congruent. Rezultatul este obținut prin concatenarea a două fragmente de 32 biți:
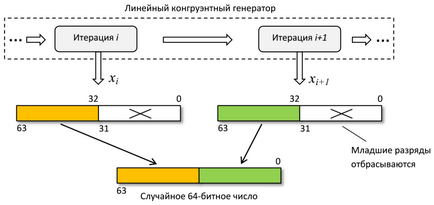
De exemplu, java.util.Random folosește același principiu, deși pentru că m = 2 48. numai biții de ordin inferior sunt eliminați acolo când se generează int și lung. Acest lucru, desigur, afectează în mod negativ calitatea numerelor aleatoare.
Aici este un exemplu de numere de secvență de 64 de biți, care se obține atunci când a = 6364136223846793005, c = 1442695040888963407, m = 2 64. x0 = 0 așa cum este descris în Figura mod:
1442695037175000593
11166244415259155177
7076646891078057782
1459328390042580878
8905969149530007863
11682375496967736740
897247724006084730
Cum sunt aleatoare aceste numere? Aproximativ la nivelul RNG din biblioteca standard Java, poate chiar mai ușor. Calculul fiecărui număr necesită doar două operații de multiplicare.
Dacă sunt necesare mai multe generatoare diferite, ar trebui alese alte valori ale constantelor a și c. calculat pentru m = 2 64. Articolul de pe această legătură oferă exemple de trei constante cu "calități bune":
c - impar, m = 2 64