Subiectul și sarcinile geodeziei
Geodezie - știința măsurătorilor de pe suprafața pământului, realizată pentru a determina forma și dimensiunile Pământului, elaborarea de planuri și hărți, precum și rezolvarea diferitelor probleme de inginerie pe teren.
Definiția formei și dimensiunilor Pământului este inclusă în sarcinile geodeziei superioare. Întrebările legate de elaborarea planurilor și a hărților și cu decizia de probleme de inginerie se referă la o geodezie.
Lucrările geodezice sunt împărțite în câmp și camerale.
Lucrările de teren constau în măsurări ale unghiurilor orizontale și verticale, ale distanțelor orizontale, verticale și înclinate. Lucrările camerale constau în calcule ale rezultatelor măsurătorilor de câmp și ale construcțiilor grafice.
Geodezia este strâns legată de o serie de alte științe - matematică, fizică, astronomie, geografie, geologie, geomorfologie etc.
Geodezie inginerie - rezolvă probleme legate de:
· Construirea unei baze geodezice de referință pentru lucrări de topografie și rupere;
· Elaborarea de planuri și profile de mari dimensiuni pentru proiectarea structurilor de inginerie;
· Producția de lucrări de amenajare în termeni de înălțime pentru construcția de clădiri și structuri;
· Întreținerea operațiunilor de construcție și instalare;
· Elaborarea desenelor executive ale obiectelor;
· Observarea deformărilor în timpul construcției.
Informații de bază despre forma și dimensiunile Pământului
Subiectul geodeziei este proprietățile geometrice ale suprafeței Pământului.
Suprafața fizică a Pământului este formată din suprafața solului și a apei și are o formă complexă.
O idee generalizată a formei Pământului poate fi obținută prin utilizarea conceptului de "suprafață plană".
O suprafață plană este o suprafață închisă care înconjoară Pământul, de la linii verticale la oricare dintre punctele sale.
În geodezie, suprafața plană, care coincide cu nivelul mediu al oceanelor în repaus, are o semnificație deosebită. O astfel de suprafață închisă, continuată sub continentele perpendiculare pe direcția liniei de plumb în fiecare punct, se numește suprafața planului la sol.
Corpul delimitat de suprafața de bază se numește geoid.
Geoidul nu coincide cu nici o figură matematică și este o formă neregulată.
Forma matematică a Pământului corespunde suprafeței unui elipsoid, care se numește referință - Krasovsky elipsoidală.
Poziția punctelor de pe suprafața pământului este determinată în diferite sisteme de coordonate:
· Sistemul de coordonate geografice - meridianul Greenwich și planul ecuator sunt considerate ca punct de plecare.
· Sistemul de coordonate geodezice determină poziția punctelor pe suprafața elipsoidului de rotație.
· Sistemul zonal al coordonatelor Gaussian rectangulare (figura 1).
Pentru a stabili relația dintre coordonatele geografice și rectangulare, aplicați o metodă de proiectare a suprafeței globului pe un plan prin părți, numite zone (fig.1). Contul de zone este condus la est de meridianul Greenwich.
Înainte de a proiecta o astfel de zonă pe un plan, aceasta este proiectată pe suprafața cilindrului. Apoi, cilindrul este desfășurat pe plan și imaginea proiecției acestei zone este obținută pe acesta. O astfel de proiecție se numește proiecția Gauss-Kruger.
Într-un astfel de sistem, originea pentru toate zonele este luată la punctul de intersecție a meridianului axial al zonei date cu ecuatorul. Axele de coordonate sunt axa abscisa-X și axa Y a ordinii (figura 2).
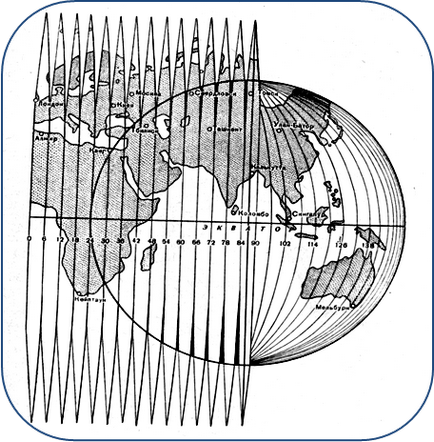
Fig. 1 Divizare în zone
Abscisa, măsurată de la ecuator la polul nordic, este considerată pozitivă, la sud - negativă. Valorile ordinii de la meridianul axial la est sunt pozitive, spre vest - negative.
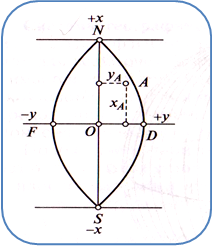
Fig.2. Sistem de coordonate zonal
· Sistem de coordonate dreptunghiulare (figura 3).
În geodezie, axa abscisei se îndreaptă spre direcția meridianului axial medial al zonei, iar axa y este direcția ecuatorului.
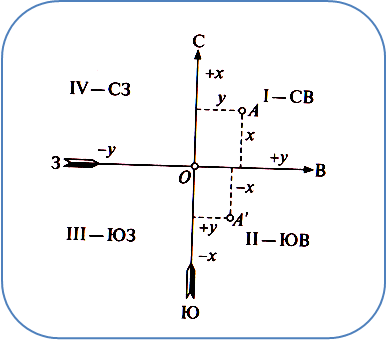
Fig. 3 Sistem de coordonate dreptunghiulare
Axele coordonatelor împart planul desenului în patru părți, numite sferturile de coordonate: I - CB, II - SE, III - SW, IV - WS (Fig.3).
· Sistemul de coordonate polar.
Poziția oricărui punct pe plan este determinată de vectorul de rază - r și de unghiul - # 946; numărate în direcția acelor de ceasornic din linia - OX (axa polare) la vectorul de rază (figura 4).
Fig.4 Sistemul de coordonate polar
Înălțimile punctelor pot fi absolute și condiționate. Dacă înălțimea unui punct este determinată de suprafața plană, atunci este considerată absolută. De la orice altă suprafață - condiționată.
Depășind (h) este diferența dintre înălțimile punctelor.
Valorile numerice ale înălțimilor punctelor sunt numite elevații.
În Rusia, înălțimile punctelor sunt măsurate de la nivelul Mării Baltice.
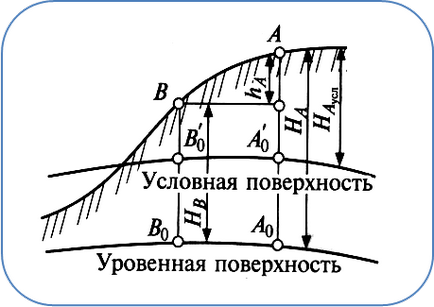
Fig. 5 Semne absolute și convenționale.