1. Manifestarea forțelor elastice și natura lor
După cum știți deja din cursul fizicii din școala principală, forțele de elasticitate sunt asociate cu deformarea corpurilor, adică prin schimbarea formei și a dimensiunilor lor.
Deformarea corpurilor legate de forțele de elasticitate nu este întotdeauna vizibilă (vom discuta acest lucru mai detaliat mai jos). Din acest motiv, proprietățile forțelor elastice sunt de obicei studiate, folosind arcuri pentru claritate: deformarea lor este vizibilă în ochi.
Vom încărca greutatea arcului (figura 15.1, a). (Vom presupune că masa arcului poate fi neglijată.) Arcul va fi întins, adică deformat.
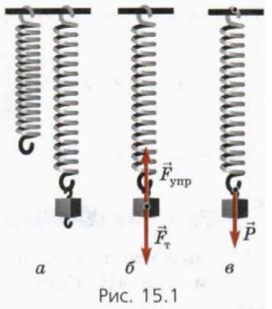
În sarcină suspendată care acționează gravitația m și aplicată de forța arcului de tracțiune a exercițiului elastic (Fig. 15.1, B). Este cauzată de deformarea arcului.
Conform celei de-a treia legi a lui Newton, forța care acționează pe partea de încărcare este același modulo, dar direcția opusă (Figura 15.1, c). Această forță - greutatea sarcinii: este forța cu care corpul se întinde vertical ridicat (arc).
Forțele de control, cu care încărcarea și primăvara interacționează una cu cealaltă, sunt legate de a treia lege a lui Newton și, prin urmare, au aceeași natură fizică. În consecință, greutatea este, de asemenea, o forță de elasticitate. (Acționând pe forța arcului de încărcare din partea arcului (greutate de sarcină), datorită sarcinii de deformare deformație imperceptibil, în cazul în care sarcina este o greutate sau bar, puteți ca o sarcină de a lua un arc masiv pentru a încărca tulpina a devenit prea vizibile: .. Vedem că va extinde. ) Acționând asupra primăverii, greutatea încărcăturii îl întinde, adică determină deformarea sa. (Pentru a evita neînțelegerile, subliniem încă o dată că primăvara, la care sarcina este suspendată, nu se întinde aplicată forța sarcinii de greutate al sarcinii și atașat la arcul de forța arcului de sarcină (greutate de sarcină).)
În acest exemplu, vedem că forțele de elasticitate sunt atât o consecință, cât și o cauză a deformării elastice a corpurilor:
- în cazul în care corpul este deformat, atunci partea acestui corp, forța elastică (de exemplu, forța exercitarea în figura 15.1, b);
- dacă forțele elastice sunt aplicate corpului (de exemplu, forța din Figura 15.1, c), atunci acest corp este deformat.
1. Care dintre forțele descrise în Figura 15.1
a) contrabalansați reciproc dacă mărfurile se află în stare de repaus?
b) au aceeași natură fizică?
c) sunt legate de a treia lege a lui Newton?
d) încetează să fie egal în valoare absolută, dacă încărcătura se va mișca cu accelerație îndreptată în sus sau în jos?
Deformarea corpului este întotdeauna vizibilă? După cum am mai spus, caracteristica "insidioasă" a forțelor elastice este că deformarea asociată a corpurilor nu este întotdeauna vizibilă.
Deformarea mesei, datorită greutății mărului care se află pe ea, este invizibilă pentru ochi (Figura 15.2).
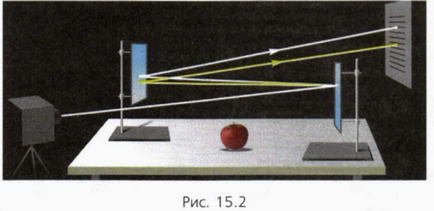
Și totuși este: numai datorită forței elastice, care a apărut ca urmare a unor deformări ale mesei, deține un măr! Deformarea mesei poate fi detectată printr-un experiment ingenios. In figura 15.2 liniile albe indică schematic progresul fasciculului de lumină, atunci când nu există nici un măr și linii galbene - cursul fasciculului de lumină, atunci când mărul este pe masă.
2. Luați în considerare figura 15.2 și explicați, astfel încât deformarea tabelului ar putea fi observată.
Un pericol este că, fără a observa deformarea, nu puteți observa forța elastică asociată!
Astfel, în condițiile unor probleme, apare un "fir inextensibil". Sub aceste cuvinte înseamnă că doar neglijabil fir de cantitate (tulpina crește lungimea sa), dar este imposibil să neglijeze forțele elastice aplicate la filamentul sau curentul de filament. De fapt, nu există niciun "fir absolut inextensibil": măsurătorile exacte arată că orice fir este cel puțin puțin, dar se întinde.
De exemplu, dacă în experimentul descris mai sus, cu o sarcină atașată la un arc (vezi. Fig. 15.1), înlocuiți arcul „firul inextensibil“, apoi pe sub firul de întindere de sarcină în greutate, cu toate că deformarea acesteia și va fi insesizabile. Și, prin urmare, toate forțele elastice luate în considerare vor fi de asemenea prezente. Forța de elasticitate a arcului va fi forța de tensionare a firului, îndreptată de-a lungul firului.
3. Fa desene figura 15.1 (a, b, c), înlocuirea arcului fir inextensibil corespunzătoare. În desene, indicați forțele care acționează asupra filetului și a sarcinii.
4. Două persoane trag coarda în direcții opuse cu o forță de 100 N fiecare.
a) Care este forța de tracțiune a frânghiei?
b) Se va schimba forța de întindere a coardei dacă un capăt este legat de un copac, iar celălalt capăt este tras cu o forță de 100 N?
Natura forțelor elastice
Forțele de elasticitate sunt determinate de forțele de interacțiune ale particulelor, din care constă corpul (molecule sau atomi). Atunci când corpul este deformat (schimbați dimensiunea sau forma acestuia), distanțele dintre particule se schimbă. Ca urmare, forțele apar între particule, care tind să readucă corpul într-o stare nedeformată. Aceasta este forța elasticității.
2. Legea lui Hooke
Vom suspenda aceleași greutăți la primăvară. Observăm că extensia arcului este proporțională cu numărul de greutăți (Figura 15.3).
Aceasta înseamnă că deformarea arcului este direct proporțională cu forța elasticității.
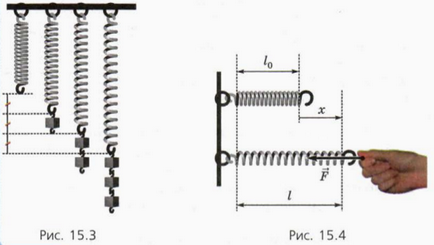
Indicați deformarea (întinderea) arcului
unde l este lungimea arcului deformat și 10 este lungimea arcului nedeformat (Figura 15.4). Atunci când arcul este întins, x> 0 și proiecția forței elastice care acționează asupra părții arcului Fx <0. Следовательно,
„Minus“ semn în această formulă reamintește că, aplicată de forța elastică a corpului deformat este îndreptată opus deformării corpului: arcul întins tinde să comprime și concis - întindere.
Coeficientul k este numit rigiditatea arcului. Rigiditatea depinde de materialul primăverii, dimensiunea și forma acesteia. Unitate de duritate 1 N / m.
Valoarea (2) este numită legea lui Hooke în onoarea fizicianului englez Robert Hooke, care a descoperit acest model. Legea lui Hooke este valabilă fără prea multă deformare (cantitatea de deformare admisă depinde de materialul din care se face corpul).
Formula (2) arată că modulul de elasticitate F este legat de modulul de deformare x de relația
Din această formulă rezultă că graficul funcției F (x) este un segment de linie dreaptă care trece prin origine.
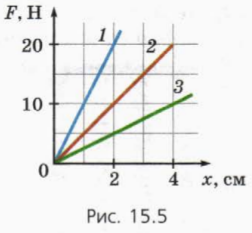
5. Figura 15.5 prezintă schemele modulului de elasticitate față de modulul de întindere pentru trei arcuri.
a) Care arc are cea mai mare rigiditate?
(b) Care este rigiditatea celui mai moale izvor?
6. Ce greutate trebuie suspendată la un arc cu o rigiditate de 500 N / m, astfel încât extensia arcului să devină egală cu 3 cm?
Este important să distingem extensia arcului x de lungimea lui l. Diferența dintre ele arată formula (1).
7. Când arcul este suspendat de o greutate de 2 kg, lungimea sa este de 14 cm, iar când este suspendat de la o greutate de 4 kg, lungimea de primăvară este de 16 cm.
a) Care este rigiditatea primăverii?
b) Care este lungimea izvorului nedeformat?
3. Cuplarea arcurilor
Conexiune serial
Luăm un arc cu rigiditate k (figura 15.6, a). Dacă îl întindem prin forță (Figura 15.6, b), elongația sa este exprimată prin formula
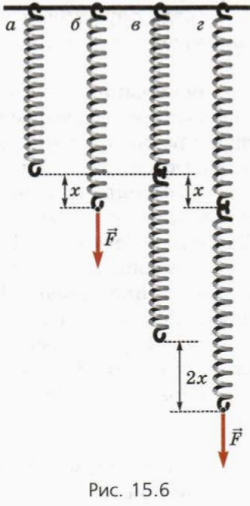
Acum luăm cel de-al doilea același izvor și conectăm arcurile, așa cum se arată în figura 15.6, c. În acest caz, ei spun că arcurile sunt conectate în serie.
Să găsim rigiditatea k a sistemului a două arcuri conectate în serie.
Dacă sistemul de primăvară forță de întindere, forța fiecărui modul de elasticitate arc este egal cu F. Alungirea totală a sistemului de arcuri este egal cu 2x, astfel încât fiecare arc va alungi cu x (fig. 15,6 g).
unde k este rigiditatea unui arc.
Deci, rigiditatea unui sistem de două arcuri de serie identic este de 2 ori mai mică decât rigiditatea fiecăruia dintre ele.
Dacă arcurile cu rigiditate diferită sunt conectate în serie, atunci forțele elastice ale arcurilor vor fi aceleași. Și alungirea totală a sistemului de arcuri este egală cu suma alungirilor arcurilor, fiecare dintre acestea putând fi calculată folosind legea lui Hooke.
8. Dovada ca atunci cand cele doua arcuri sunt conectate in serie
1 / kpos = 1 / k1 + 1 / k2. (4)
unde k1 și k2 sunt rigiditatea arcului.
9. Care este rigiditatea unui sistem de două arcuri conectate în serie de 200 N / m și 50 N / m?
În acest exemplu, rigiditatea sistemului de două arcuri conectate în serie sa dovedit a fi mai mică decât rigiditatea fiecărui arc. Este întotdeauna așa?
10. Dovada că rigiditatea unui sistem de două arcuri conectate în serie este mai mică decât cea a oricărei arcuri care formează sistemul.
Conexiune paralelă
Figura 15.7 din stânga arată arcuri identice în paralel.
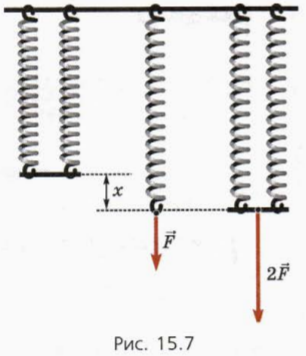
Indicăm rigiditatea unui arc k și rigiditatea sistemului de arc kpar.
11. Dovedeste ca kpar = 2k.
O sugestie. Vezi Figura 15.7.
Deci, rigiditatea sistemului de două izvoare paralele conectate este de 2 ori mai mare decât rigiditatea fiecăruia dintre ele.
12. Descoperiți că atunci când conectați paralel două arcuri de rigiditate k1 și k2
O sugestie. Cu conexiunea paralelă a arcurilor, alungirea lor este aceeași, iar forța elastică care acționează pe partea sistemului de arcuri este egală cu suma forțelor lor elastice.
13. Două arcuri cu o rigiditate de 200 N / m și 50 N / m sunt conectate în paralel. Care este rigiditatea unui sistem de două izvoare?
14. Dovada că rigiditatea sistemului de două arcuri conectate paralel este mai mare decât cea a oricărei arcuri care formează sistemul.
Întrebări și sarcini suplimentare
15. Construiește un grafic al dependenței modulului de elasticitate de alungire pentru un arc cu o rigiditate de 200 N / m.
16. Un coș cu o masă de 500 g este tras pe masă cu un arc de 300 N / m, aplicând forța orizontală. Frecarea între roțile coșului și masă poate fi neglijată. Care este extensia arcului dacă căruciorul se mișcă cu o accelerație de 3 m / s 2?
17. O greutate de m este suspendată de arc de rigiditatea k. Care este prelungirea arcului când sarcina este în repaus?
18. Arcul de rigiditate k a fost tăiat în jumătate. Care este rigiditatea fiecărei arcuri formate?
19. Arcul de rigiditate k a fost tăiat în trei părți egale și conectat în paralel. Care este rigiditatea sistemului de primăvară?
20. Dovediți ca rigiditatea izvoarelor identice conectate în serie să fie de n ori mai mică decât rigiditatea unui arc.
21. Să demonstreze că rigiditatea n a izvoarelor identice conectate paralel este de n ori rigiditatea unui arc.
22. Dacă două arcuri sunt conectate în paralel, rata de primăvară a sistemului este de 500 N / m, iar în cazul în care același izvor conectat în serie, rata de primăvară a sistemului este de 120 N / m. Care este rigiditatea fiecărui primăvară?
23. Barul situat pe o masă netedă este fixat pe suporturi verticale cu arcuri de 100 N / m și 400 N / m (Figura 15.8). În starea inițială, arcurile nu sunt deformate. Ce va face forța elastică care acționează asupra barei dacă se mișcă 2 cm spre dreapta? 3 cm în stânga?