"Cum va spune măsura și frumusețea" - pagina №1 / 1
Lecție integrată de matematică și IZO (programul "Arte vizuale și lucrări de artă") pentru clasa a 6-a
Nikitina Tatiana Ivanovna, profesor de matematică
Tema lecției: "Cum va spune măsura și frumusețea".
Pe exemplul obiectelor din viața de zi cu zi, arta aplicată și arhitectura de diferite vremuri, pentru a permite copiilor să înțeleagă că, prin reprezentarea lumii obiective, artiștii au exprimat întotdeauna o înțelegere a valorilor timpului lor.
Să se familiarizeze cu conceptul de "Secțiunea de Aur", valoarea sa numerică
Arătați aplicarea practică a cunoștințelor și abilităților pe tema "Proporție" pe exemplul "secțiunii de aur"
Să promoveze cunoașterea legilor frumuseții și armoniei lumii înconjurătoare.
A învăța să creezi o schiță a unui obiect cu mijloace de aplicație și ornament.
Echipament:
prezentare pentru lecție;
riglă, creion simplu, busole;
o foaie de hârtie de peisaj, hârtie colorată;
lipici, foarfece.
Moment organizatoric.
Tema lecției de astăzi este "Cum va spune măsura și frumusețea"
În lecție vom vorbi despre proporție, vom învăța să aplicăm cunoștințele noastre pentru proiectarea și decorarea templului. Profesorul artelor plastice ne va ajuta.
Conversație la interviu (profesor IZO):
Toată lumea este un artist prin natură. În procesul de muncă umană se naște lucruri frumoase și necesare. Ele sunt create de mâinile omenești.
Dar cum a apărut capacitatea unei persoane de a crea frumusețe?
Primul profesor în această afacere a fost un om de natură. Urmărind imaginile naturii, un om învățat de la ea.
Peisajele sale multicolore și discrete de vară au inspirat persoana să se înconjoare nu numai cu lucruri necesare, dar utile, dar frumoase. Slide 2
O culoare frumoasă (roșie) în Rusia a fost mult timp considerată magică. Prin urmare, există atât de multe dintre ele pe articole de uz casnic (un dulap, obiecte de veselă). Diapozitivele 3, 4
Admirați florile, un bărbat le-a decorat cu imagini ale zidurilor de temple și vase, covoare și tăvi. Slide 5
Modelele înghețate pe fereastra de iarnă au inspirat executarea unor broderii frumoase (alb pe alb) și dantele (faimoasa dantelă Vologda). Slide 6
Imagini de animale și de păsări au fost transferate pe pereții bisericilor, prosoapelor și jucăriilor.
Natura este conducătorul creatorului.
Și au lucrat meșteșugari în Rusia din cele mai vechi timpuri, conform regulii:
"Cum va fi spus MERA și BEAUTY"
Măsurarea este o măsurătoare, adică frumoase, proporții precise (Biserica Adormirii de la Kondopoga, Biserica de mijlocire pe Nerl). Diapozitivele 8, 9
O formă frumoasă frumoasă este bună în sine, dar nu este rău să subliniezi decorarea, decorarea (forma porții, cupola bisericii) Diapozitive 10, 11, 12
IIIntroducere material (profesor de matematică):
repetiție
Dar chiar și fără finisare specială, ele sunt bune, proporții atât de clare.
Ce se numește proporția? (Egalitatea a două relații)
Înregistrați proporția utilizând literele (a.b = c.d sau)
Citiți proporția
Denumiți proprietatea de bază a proporției
Se pare că printre proporțiile care sunt deosebit de atractive pentru ochi, cea mai faimoasă "SECȚIUNEA GOLDENĂ"
Istoricul istoric:
Secțiunea de aur este o combinație de proporții, în care cele mai armonioase, frumoase ne par a fi clădiri, sculpturi, alte produse și chiar muzică. Aceste proporții sunt alese nu numai prin intuiție, ci pot fi calculate.
Termenul "secțiunea de aur" a fost folosit pentru prima dată de marele artist și inginer Leonardo da Vinci, care a studiat și a lăudat proporția de aur pe toată durata vieții sale.
Secțiunea de aur, diviziunea sau împărțirea armonică a unui segment în raportul extrem și mijlociu este împărțirea unui segment în două părți inegale, în care întregul segment se referă la cea mai mare parte a acestuia, cea mai mare la cea mai mică, adică cu: b = b: (c-b). Slide 14
Pentru a găsi b, obținem o ecuație a cărei soluție dă b = c: 2 * (√5-1) ≈ 0.618 ... * c (vom rezolva astfel de ecuații în clasa a VIII-a)
În Evul Mediu studiul secțiunii de aur a fost îmbogățită prin lucrările lui Leonardo din Pisa, poreclit Fibonacci - matematician restante italian al secolului al 18-lea. Crearea unei serii interminabile în care fiecare număr este suma dintre ultimele două (1, 2, 3, 5, 8, 13, 21, etc.), se constată că raportul dintre numere adiacente apropiate de secțiunea de aur.
Proprietățile remarcabile au un dreptunghi, ale cărui laturi corespund acestor numere. Când se împarte de pătrat și un alt dreptunghi, unde acesta din urmă păstrează același raport de aspect. Această proprietate constă în faptul că obiectul, pictura, sculptura, clădiri sau părți ale acestora într-un dreptunghi cu raportul lateral, contribuie la cele mai clare și ușor, plăcut ochiului, percepția formelor, chiar și la o distanță mare.
A întors capul - acesta este "doi".
Mâini în jos, privește în față - aceasta este "trei".
Mâinile din laturi s-au extins la "patru".
Cu forța umerilor lor de a apăsa - acesta este "cinci".
Toți băieții trebuie să se așeze - este "șase".
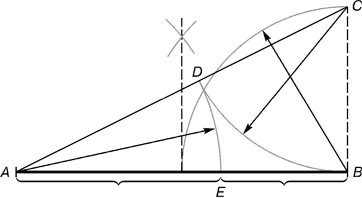
Construiți un punct E care împarte acest segment AB în raportul mediu și extrem, adică într-un raport de aur. Slide 15
Algoritmul de împărțire a unui segment într-un raport dat:
Construim un triunghi cu unghi drept, dintre care unul are de doua ori lungimea celuilalt (BC = ½ AB);
Legăm punctele A și C;
Am amânat segmentul CD = BC pe segmentul AC;
Am amânat segmentul AE = AD pe segmentul AB;
Punctul E este dorit, produce secțiunea de aur a segmentului AB
Construiți un dreptunghi cu laturile de 8 cm și 3 cm în notebook-uri
Împărțiți lungimea dreptunghiului în două părți într-un raport de 5: 3
Împărțiți dreptunghiul în două părți, adică Conectați punctele rezultate la lungimile acestui dreptunghi
Avem un dreptunghi, laturile cărora sunt într-un raport de aur, adică raportul dintre lățime și lungime indică numărul ≈ 0,62 (verificare: 3: 5 = 0,6). Un astfel de dreptunghi se numește dreptunghi de aur
VI Aplicarea abilității de a diviza segmentul într-un raport de aur (profesor ISO):
În clasele junior am cunoscut deja creativitatea arhitecturală a vechilor maeștri din Novgorod, Vladimir, Suzdal etc. a lucrat la tăierea unei biserici cu un singur loc. Slide 16
Dacă mai devreme am lucrat cu dvs. intuitiv, prin ochi, atunci astăzi putem deja calcula raportul dintre segmente într-un raport de aur.
Activitatea 1:
O foaie de hârtie dreptunghiulară albă este împărțită în două părți într-un raport de 3: 5;
pliere dublă pe verticală;
un mod de excizie simetrică pentru a realiza silueta unei biserici cu un singur cupol. Slide 17
Sarcina creativă:
Modificați silueta elementelor decorative cu templul unic.
VIITotă lecție (profesor de matematică):
Expoziție de lucrări pentru copii. Slide 18
Cum este divizată segmentul citit într-un raport de aur?
Ce dreptunghi se numește aur?
VII Tema:
Găsiți în lumea din jur exemple de proporții de aur.
Referințe: