Conform ecuației, se face o schemă:
Figura 1.2. Tipul schemei de simulare pentru obținerea unei traiectorii de fază
Pentru a construi o cale, utilizați blocul XY Graph din secțiunea Sinks. Intrarea sistemului este 0 prin intermediul blocului Constant din secțiunea Surse. În setările sale, valoarea constantă este setată la "0".
Condițiile inițiale sunt setate în setările integratorului. Valoarea dorită este setată în câmpul Stare inițială. Valoarea inițială a funcției este stabilită pentru integratorul, la ieșirea căruia funcția y. Valoarea inițială a derivatului este pentru cea cu derivat la ieșire. Condițiile inițiale (0,0) nu sunt adecvate. În acest caz
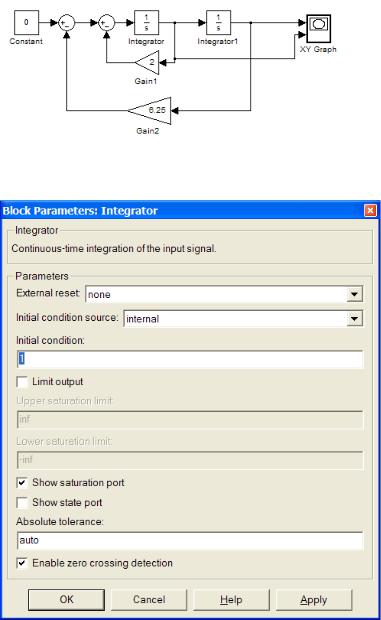
soluția ecuației este funcția y = 0, y 'este, de asemenea, zero. Întreaga traiectorie de fază va fi un punct (0,0), și nimic nu poate fi judecat din ea. De obicei, se iau condițiile inițiale (1.1).
Pe el se face circuitul:
Figura 1.7. Un fel de sistem de modelare a unui sistem de ordinul trei pentru a obține o traiectorie de fază
Condițiile inițiale sunt stabilite pentru toți cei trei integratori.
2. Modelarea sistemelor neliniare
Este de asemenea posibil să se construiască traiectorii de fază pentru sisteme cu elemente neliniare. Partea liniară a unui astfel de sistem este reprezentată în același mod ca și cele descrise mai sus și înainte de acesta este inclus un element neliniar. În Simulink, majoritatea elementelor neliniare sunt situate în secțiunea Discontinuități.
Există astfel de elemente neliniar ca:
- Releu - releu cu histerezis. Setările specifică "Punct de pornire", "Punct de oprire" - valorile de intrare la care releul comută de la joasă la înaltă și de la mare la joasă. Dacă valorile sunt identice, nu va exista nici o histereză. "Ieșirea atunci când este activată" și "Ieșirea când este oprită" sunt cele ridicate și scăzute
Zona Dead - un element cu caracter liniar și cu o bandă mortală. Setările indică limitele zonei neconectate.
- Saturația este un element cu caracteristică liniară și saturație. Setările specifică valorile la care are loc saturația.
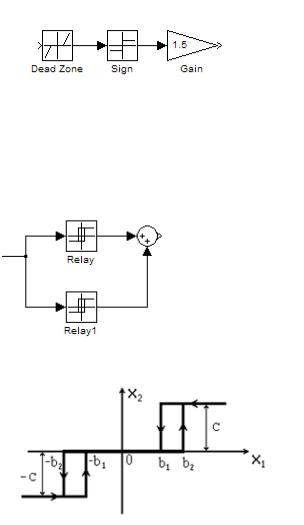
În plus, atunci când creați modele de sisteme neliniare, este posibil să aveți nevoie de un bloc de semne din secțiunea Operații matematice. Dacă o valoare negativă este introdusă la intrare, blocul va fi -1, 0 va fi 0 când este alimentat și unul pozitiv la ieșirea unității.
Pentru a obține un releu cu o bandă de bandă nefuncțională, trebuie să conectați în serie blocurile Dead Zone și Sign. Limitele zonei neconectate sunt indicate în setările Zonei Dead. În cazul în care nivelul de ieșire ar trebui să fie diferit de unul, un amplificator este plasat pe ieșire.
Figura 2.1. Modelul releului cu bandă mortală
Releele cu bandă mortală și histereză pot fi obținute prin însumarea semnalelor de la două relee.
Figura 2.2. Modelul unui releu cu bandă mortală și histereză.
Figura 2.3. Releu caracteristic cu bandă mortală și histereză.
Pentru primul releu, un punct de pornire este setat la egal cu b 2. Punctul de oprire - egal cu b 1 Valoarea de nivel înalt "Ieșire când este pornit" este egală cu c, iar valoarea mică este 0.
Pentru cel de-al doilea releu, "Punctul de pornire" este setat la -b 1., iar punctul "Oprire" înseamnă -b 2 Valoarea nivelului ridicat "Ieșirea atunci când este activată" este 0 și valoarea scăzută este -c.
De exemplu, b1 = 1, b2 = 2, c = 0,5.
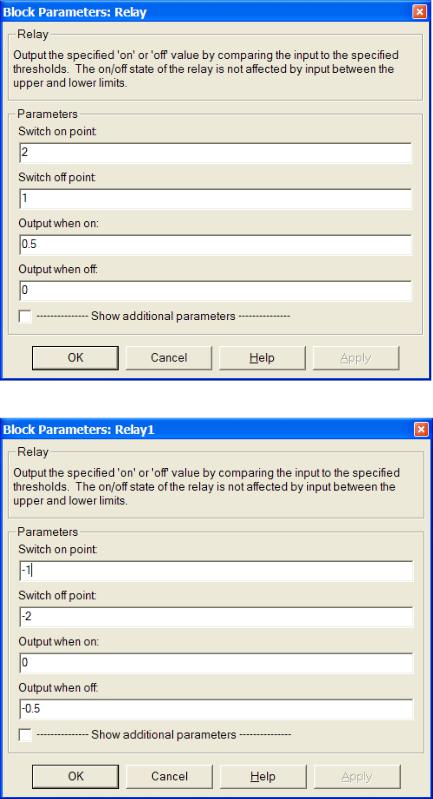
Fig.2.4. Setarea primului releu.
Figura 2.5. Setarea celui de-al doilea releu.
Fiind capabil să construiască traiectorii de fază pentru sisteme liniare și să modeleze elemente neliniare, se poate obține un portret de fază pentru un sistem neliniar.
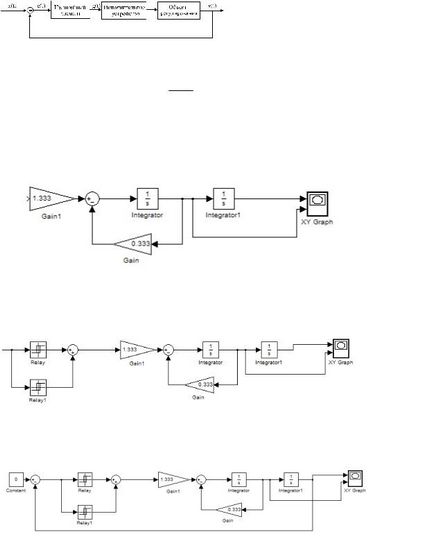
Figura 2.6. Diagrama funcțională a unui sistem neliniar.
Partea liniară a sistemului este descrisă de ecuația:
3 d 2 y 2 (t) dy (t) 4 F (y (t)). dt dt
Elementul neliniar F (y (t)) este un releu cu histereză și bandă de bandă netedă.
În conformitate cu instrucțiunile date în prima secțiune, construim schema părții liniare, oferim condițiile inițiale pentru integratori.
Figura 2.7. Schema părții liniare a sistemului.
La intrarea în sistem, am setat elementul neliniar și l-am setat:
Figura 2.8. Schema unui sistem cu un element neliniar.
Acoperiți sistemul cu feedback și setați constantă sursa la "0":
Figura 2.9. Schema schematică a unui sistem neliniar.
În setări, specificați timpul de simulare dorit (meniul Simulare -> Parametri de simulare ... -> Timp stop) (aproximativ 200).
Făcând simularea, obținem o traiectorie de fază.
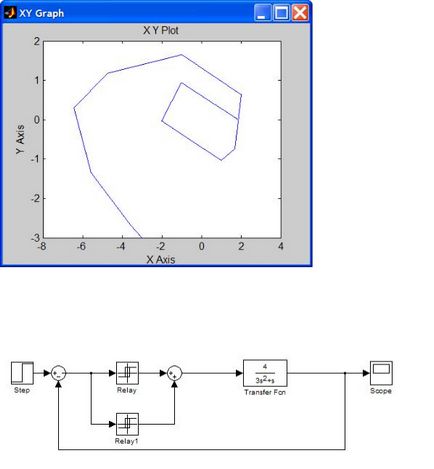
Figura 2.10. Faza traiectorie a unui sistem neliniar.
De asemenea, în conformitate cu această schemă, se poate obține un proces tranzitoriu. Pentru aceasta, blocul XY Graph este înlocuit cu Domeniul de aplicare și constanta 0 din blocul Pas. Pentru integratori, sunt setate valori inițiale zero. Sau, este posibil să se reprezinte partea liniară sub forma unei funcții de transfer.
Figura 2.11. Schema de obținere a unui proces tranzitoriu. Partea liniară este sub forma unei funcții de transfer.
Este important să rețineți următoarele: în prezența unor elemente cu bandă mortală sau histerezis, este posibil ca sistemul să nu reacționeze în nici un fel la un efect pas cu pas. Acest lucru se va întâmpla dacă valoarea de intrare pentru primul comutator (valoarea b 2 din acest exemplu) este mai mare decât una. Apoi, pentru a obține un proces tranzitoriu, fie această valoare trebuie redusă, fie o valoare mai mare pentru acțiunea pas cu pas trebuie să fie setată (modificați valoarea "Final value" din setările elementului Step). În exemplul nostru, trebuie să setați o valoare mai mare decât b 2.
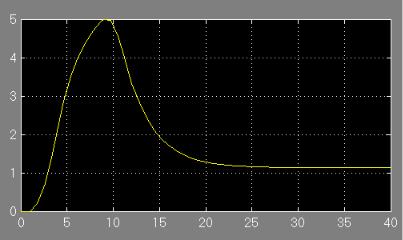
Figura 2.12. Procesul tranzitoriu al unui sistem neliniar. Valoarea "finală" pentru Step este de trei.