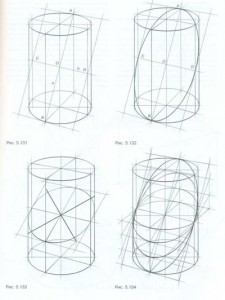
Pentru a învăța cum să construiți o secțiune oblică a unui cilindru, studiați cu atenție secvența de construcție și apoi faceți o secțiune transversală a cilindrului în primul rând și apoi - mai multe planuri înclinate.
Poziția planurilor de tăiere este dată de proiecțiile ortogonale din Fig. 5,725 și 5,126.
Secțiunea transversală a cilindrului cu un plan oblic este o elipsă. Construcția unei astfel de secțiuni se realizează în aceeași secvență ca secțiunea oblică a hexaedrului. Pentru a construi o secțiune a cilindrului cu un plan înclinat (figura 5.127), sunt necesare și două secțiuni auxiliare care trec prin axa sa verticală. Aceste secțiuni încrucișate ajută la determinarea dimensiunilor elipsei. Secțiunea auxiliară 7 este perpendiculară pe planul secant (figura 5.128). Linia de intersecție a secțiunii auxiliare 1 cu planul înclinat - linia dreaptă a (Figura 5.729) - fixează dimensiunile longitudinale ale elipsei (punctele A și B). Punctul de intersecție al acestei linii drepte cu axa verticală a cilindrului (punctul O) este centrul elipsei. Secțiunea transversală auxiliară 2 este perpendiculară pe secțiunea 7 (Figura 5.730). Linia de intersecție a planului secant oblic cu planul auxiliar 2 - linia dreaptă b - fixează dimensiunile transversale ale elipsei secțiunii (punctele C și D) (Figura 5.131). Pentru o construcție mai precisă, trageți prin punctele A,
B, C și D, ca și cum ar descrie un dreptunghi în jurul elipsei viitoare, ale cărui laturi sunt paralele cu liniile drepte a și b. Acum scrieți în acest dreptunghi o elipsă care ar trebui să atingă laturile dreptunghiului la punctele A, B, C și D, precum și formarea cilindrului (Figura 5.132). Elipsa secțiunii înclinate și a figurii dvs. prospective va fi reprezentată ca o elipsă. Cu toate acestea, trebuie remarcat faptul că axele sale nu coincid cu axele determinate de punctele A, B, C și D. Acest lucru este evident în exemplul secțiunii cilindrului prezentată în Fig. 5.133. Axele, în privința cărora elipsa este simetrică, sunt separate printr-o linie groasă în desenul în perspectivă. Acum, construiți secțiuni suplimentare ale cilindrului cu planuri înclinate.
Luați în considerare Fig. 5.734. Rețineți că toate elipsele din secțiune au un centru comun. Analizați modul în care se modifică dimensiunile elipticelor secțiunii când se schimbă poziția planului de tăiere. Dimensiunea transversală a elipsei rămâne constantă, însă dimensiunea longitudinală se schimbă, iar cu cât este mai verticală planul secant, cu atât este mai mare. Aproximarea planului de tăiere în poziția orizontală reduce dimensiunea longitudinală până când devine egală cu dimensiunea transversală, apoi elipsa secțiunii se transformă într-un cerc. În consecință, zona secțiunii transversale se modifică. Secțiunea orizontală, cu cât suprafața este mai mică, cu o creștere a unghiului de înclinare, crește și zona secțiunii transversale.
Secțiunea înclinată a cilindrului
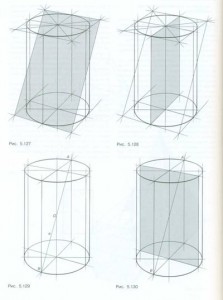
Secțiunea înclinată a cilindrului