2 Ce este simetria? Care este simetria centrală? Exemple de simetrie centrală.

3 Definiția simetriei: Două puncte A și A1 sunt considerate a fi simetrice în raport cu punctul O dacă G este punctul central al segmentului AA1. Punctul O este presupus a fi simetric cu el însuși. Definiția simetriei: Două puncte A și A1 sunt considerate a fi simetrice în raport cu punctul 0 dacă G este punctul central al segmentului AA1. Punctul O este presupus a fi simetric cu el însuși.

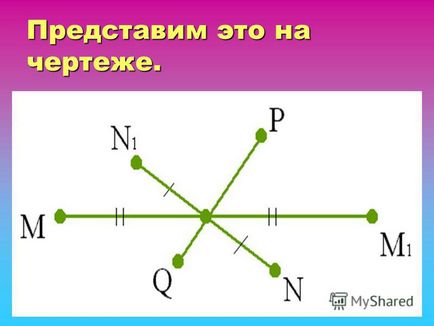
4 Exemplu: puncte Figura M și M1, N și N1 sunt simetrice cu punctul O, iar punctele P și Q nu sunt simetrice în raport cu acest punct Exemplu: Figura punctele M și M1, N și N1 sunt simetrice cu punctul O, iar punctele P și Q nu sunt simetrice în ceea ce privește acest punct

5 Să ne imaginăm acest lucru în desen.
6 Definirea simetriei centrale: O cifră se spune a fi simetrică cu privire la punctul O, dacă pentru fiecare punct al figurii punctul care este simetric față de el în raport cu punctul O aparține, de asemenea, acestei cifre. Punctul O este numit centrul simetriei figurii. Se mai spune că cifra are o simetrie centrală. O cifră se spune a fi simetrică cu privire la punctul O, dacă pentru fiecare punct al figurii punctul care este simetric față de punctul O aparține, de asemenea, acestei cifre. Punctul O este numit centrul simetriei figurii. Se mai spune că cifra are o simetrie centrală.

7 Voi da exemple de figuri cu simetrie centrală. Cele mai simple figuri cu simetrie centrală sunt un cerc și o paralelogramă.

8 Centrul de simetrie al unui cerc este centrul unui cerc

9 Un centru de simetrie a paralelogramului este punctul de intersecție a diagonalelor sale.

10 Direct de asemenea, are o simetrie centrală, dar în contrast cu cercul și un paralelogram, care au doar un singur centru de simetrie (punctul D în figură), în linie dreaptă, sunt infinit de multe - orice punct al liniei este centrul de simetrie. Un exemplu de figura care nu are un centru de simetrie este un triunghi.

11 Exemple de simetrie centrală.
12
13