12.7.1. Metoda cilindrilor
Metoda Cylinder constă în aceea că această suprafață de rotație este împărțit cu ajutorul unui meridian relativ îngust egale între ele cotă, atunci fiecare astfel de fracțiune este înlocuită suprafață cilindrică descrisă care atinge suprafața meridianul central de la punctele lobe (Fig. 159). Limitele suprafeței cilindrice vor fi planurile meridianelor, care limitează fracția considerată.
Luați în considerare aplicarea acestei metode pentru a construi o maturare a suprafeței unei sfere.
Împărțiți sfera prin intermediul meridianelor în șase părți egale (Figura 160). Fiecare dintre piesele formate este proiectată pe P1 sub forma sectorului I1 -41-II1. Să luăm în considerare construcția cursei condiționale a unei părți a sferei, meridianul mijlociu al căruia este principalul meridian. Mai întâi, această parte a sferei este înlocuită de suprafața cilindrică Ф (Ф1, Ф2), descrisă în apropierea ei.
Formarea unei suprafețe cilindrice a cărei axă este q (q1, q2) ⊥ Π2. sunt linii drepte proiectate în față. Proiecția orizontală a acestui element cilindric este triunghiul ΔA1 B1 O1. iar proiecția frontală este conturul sferei. Figura 159 prezintă o reprezentare grafică a unui cilindru care înlocuiește o parte a sferei.
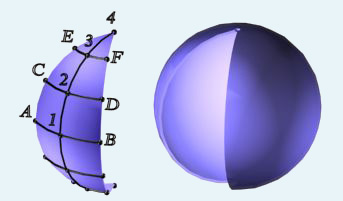
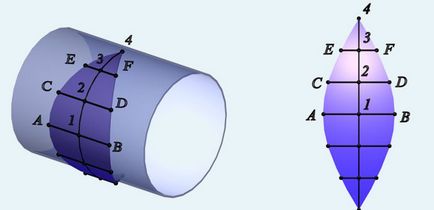
Fig. 159. Metoda cilindrilor
Pentru a construi această suprafață cilindrică (lobe) vedere frontală l2 scanare de meridianul principal este de a fi divizat în șase părți egale de către punctele 1, 2, 3, 4 ... și naviga prin punctele de diviziune proiecție orizontală care formează suprafața cilindrică. Apoi, este nevoie să meridian „îndrepta“, adică arcul 1-2, 2-3, 3-4 pentru a înlocui acordurile 12 -22. 22 -32. 32 -42. În acest scop, P1 plan prin punctele 1, 2, 3, 4 pentru a ține arcul în termen de o lungime bate, și înlocuiți tangenta respectivă a fiecărui arc A1 B1. C1 D1. E1 F1.
Pentru a trasa o scanare a uneia dintre cele șase părți într-o locație arbitrară, trageți o axă verticală a simetriei și așezați segmentele 12-22 pe ea. 22 -32. 32 -42 de la planul P2. adică lungimea generatorului de schițe, înlocuită cu acorduri:
Prin punctele 10. 20. 30. 40 pentru a trasa linii orizontale și pentru a amâna pe ele următoarele segmente:
Prin conectarea punctelor obținute printr-o curbă netedă cu o linie, este dezvoltată o parte a acestei sfere, egală cu 1/6 din partea sa. Dezvoltarea celorlalte acțiuni este repetarea primei. De obicei, sfera, ca orice altă suprafață de rotație, este împărțită în douăsprezece sau mai multe părți pentru a obține o scanare mai precisă.
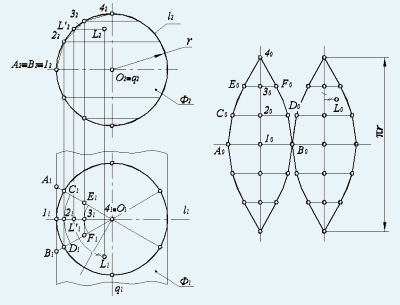
Fig. 160. Construcția unei maturi a unei sfere prin metoda cilindrilor
Pentru a pune la punct L scanare (vezi. Fig. 160), aparținând domeniului, trebuie mai întâi rotit pentru a se alinia cu principalul meridianul l, obținând L „(L'1. L'2). Apoi măsurați P2 distanța pe poziția rotită a punctului L (L'2) până la cea mai apropiată meridianul despărțitor (în acest caz, distanța L'2 32) și la un P1 distanța măsurată de la punctul L la proiecția proporția medie de meridianul pe care punctul L .
Folosind aceste două distanțe, punctul L0 este construit pe baza dezvoltării fracțiunii dorite. corespunzând unui anumit punct L (egalitatea segmentelor corespunzătoare este indicată prin simboluri speciale).
Să luăm în considerare construcția unei curse prin metoda cilindrilor, pe exemplul unei suprafețe de torus (1/4 din inel) (figura 161):
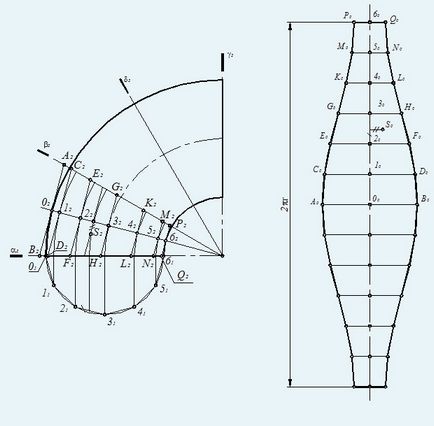
Fig. 161. Construcția unei curse a inelului prin metoda cilindrilor
1. Împărțiți suprafața inelului de către planurile β (β2), δ (δ2) ... în părți egale. Drept rezultat, întreaga suprafață a inelului este împărțită în douăsprezece părți egale, dintre care numai trei sunt prezentate în figura 161.
Fiecare dintre părți este înlocuită cu suprafața unui cilindru circular drept, al cărui diametru este egal cu diametrul secțiunii inelului.
2. Construirea unui cerc - de secțiune transversală dimensiune normală de viață și împărțirea acesteia în șase părți egale de către punctele 0.1, 2, 3, 4, 5, 6. Transferul acestor puncte pe planul (final feței) ale Torul și să le transporte printr-un arc de cerc în termen de un lob (parte). Înlocuiți lungimile de arc ale lungimilor tangente: AB (A2 B2), CD (C2 D2), EF (E2 F2), GH (G2 H2), KL (K2 L2), MN (M2 N2) și PQ (P2 Q2). Astfel, lățimea de măturare este egală cu suma lungimilor tangentelor.
4. Prin aceste puncte de diviziune 00. 10. 20. 30. 40. 40. 50. 60 dețin perpendiculare pe care să se amâne următoarele segmente:
5. Conectați punctele obținute, pentru a construi maturarea unei părți a inelului.
Aplicarea punctelor arbitrare pe suprafața unui inel se face exact ca în cazul aplicării punctelor pe o maturare a unei sfere.
Figura 161 prezintă construcția unui punct S pe cursa care aparține suprafeței inelului (egalitatea segmentelor corespunzătoare este indicată prin simboluri speciale).