Să ne întoarcem la dreptunghiul nostru, pe care am început să îl luăm în considerare în articolul precedent. Suntem interesați de raportul dintre lungimile laturilor dreptunghiului și lungimile diagonale. că este, vom rezolva aceeași problemă ca
Cu toate acestea, timp de multe secole până în prezent egiptenii pe baza experienței practice, am stabilit că, dacă o parte a unui triunghi dreptunghic este egală cu 3 unități, iar celelalte - 4 unități, lungimea ipotenuzei este de 5 unități. În acest caz, raportul dintre ipotenuzei și o parte este egal cu $ \ frac54 $ pentru latura mai lungă și 5 $ \ frac53 $ pentru mai scurt.
Grecii au abordat sarcina dintr-o perspectivă mai generală. Pentru ei a fost important să găsească o regularitate, adică raportul dintre lungimea laturilor dreptunghiului și lungimea diagonalei pentru orice triunghi cu unghi drept.
După cum spune istoria, marele matematician grecesc Pitagora a descoperit acest model. El a stabilit că pentru orice triunghi cu unghi drept, următoarea afirmație este adevărată:
suma pătratelor laturilor este egală cu pătratul hipotenentei.
Această afirmație se numește teorema lui Pitagora. Teorema poartă în continuare numele marelui greacă, deși acum știm că, chiar 600 ani înainte de Pitagora, antic chinez știa deja această relație.
Să verificăm teorema pentru un triunghi cu laturile 3 și 4. Pătratul uneia dintre laturi este egal cu 3 × 3 = 9, pătratul celeilalte părți este egal cu 4x4 = 16. Suma pătratelor este 9 + 16 = 25, adică pătratul hipotensei este de 25, prin urmare, hypotenuse este egal cu 5.
Luați în considerare un alt triunghi cu laturile 5 și 12.
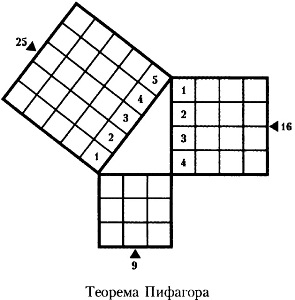
Pentru acest triunghi, raportul dintre hypotenuse și lateral este $ \ frac $ pentru partea scurtă și $ \ frac $ pentru partea lungă.
Folosind teorema lui Pythagoras. puteți găsi raportul dintre hypotenuse și oricare dintre laturile oricărui triunghi cu unghi drept. Matematicienii din Grecia antică puteau respira pașnic, sarcina a fost rezolvată. Cel mai important, teorema extinsă la toate triunghiurile dreptunghiulare, inclusiv, desigur, triunghiuri echilaterale, în care ambele părți sunt egale. Și acum suntem interesați doar de astfel de triunghiuri.
Unul dintre ele este prezentat în imaginea din stânga
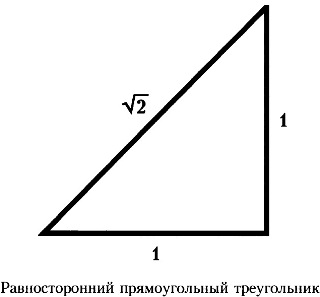
Să simplificăm problema cât mai mult posibil și să presupunem că laturile triunghiului sunt egale cu 1. Atunci pătratul lateral este 1x1, iar suma pătratelor laturilor este 1x1 + 1x1 = 2. Conform teoremei pitagoreene, pătratul hypotenusei este 2, iar hypotenuse este egal cu $ \ sqrt $, respectiv.
Materiale pe tema:
Trimiteți-le prietenilor: