Algebrele de diferite tipuri au în mod evident o structură substanțial diferită. Dacă, pe de altă parte, algebrele sunt de același tip, atunci similitudinea lor se caracterizează prin noțiunile de homomorfism și izomorfism introduse mai jos.
Să fie date două algebre
de același tip, adică ariții și; și; și - sunt la fel.
Un homomorfism al algebrei A în algebra называется este maparea -. îndeplinind următoarea condiție:
pentru toate operațiunile și -.
Înțelesul condiției (1):
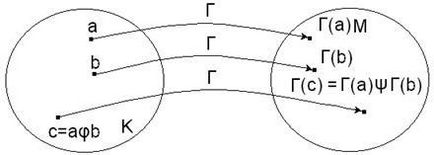
indiferent de operațiunea din setul de K efectuat mai întâi și dacă maparea este produsă apoi T sau T cartografiere produs primul și funcționarea corespunzătoare, apoi se formează setul M. rezultatul va fi același.
Un izomorfism al lui A pe algebra B este un homomorfism unu-la-unu. În acest caz, există o mapare inversă. de asemenea, una la una.
Lasă-l să fie. . Apoi. În (1), înlocuiți laturile din stânga ale acestor egalități cu laturile din dreapta și aplicați egalitatea rezultată pe ambele părți. Deci, cum. atunci primim:
Egalitatea (2) este identică cu (1) cu T înlocuită cu. elementele setului K prin elementele setului M și schimbarea locurilor u. Cu alte cuvinte, acesta este un izomorfism al lui B pe A.
Dacă există un izomorfism al A pe B. atunci există un izomorfism al lui B pe A; în plus, se consideră că algebrele A și B sunt izomorfe.
Puterile seturilor de transportoare ale algebrelor isomorfe sunt egale (sub homomorfismul pe care această egalitate nu îl poate deține).
Un automorfism pe sine și un automorfism este un homomorfism cu condiția ca A = B.
Un izomorfism în sine este un izomorfism.
1. Să fie mulțimea tuturor întregurilor; Este setul de numere întregi;
a) și sunt izomorfe. Un izomorfism este o cartografiere. în plus, condiția (1) are forma: 2 (a + b) = 2a + 2b. Deoarece. atunci G este un izomorfism al algebrei în sine.
b) harta este un automorphism pentru algebra.
Condiția (1) are forma:
c) hartă pentru o algebră nu este un automorphism, deoarece
2. Un izomorfism între algebre și este maparea (un subset pozitiv al lui R).
Condiția (1) are forma egalității:
3. algebra booleană Cantor B (U),) și B (),), format din două seturi diferite de U și izomorfe putere egală. Operațiile sunt la fel pentru ei, iar cartografia lui Γ poate fi orice corespondență unu-la-unu între U și.
Relația isomorfism este o relație de echivalență pe setul de algebre:
- reflexivitatea relației isomorfism este evidentă;
- simetria rezultă din existența unui izomorfism invers;
- tranzitivitatea stabilite după cum urmează: în cazul în care - izomorfism pe B. A - izomorfism S. In izomorfism A la C și va compoziție.
Clasele de echivalență într-o partiție în raport cu un izomorfism sunt clasele de algebre isomorfe. Conceptul de izomorfism este unul dintre cele mai importante din matematică. Esența ei, așa cum reiese din exemplele pot fi exprimate ca: Dacă A și B sunt izomorfe, elementele și operațiile în B pot fi redenumite, astfel încât B coincide cu A.
Din condiția (1) a unui izomorfism rezultă că orice relație echivalentă din algebra A este păstrată în orice algebră izomorfă pentru ea. Acest lucru face posibilă obținerea unor astfel de relații în algebra A și în mod automat să le distribuie algebră izomorfă A. comună expresie matematică „considerat până la izomorfism“ înseamnă că descrie doar proprietățile obiectelor care sunt stocate sub izomorfismul t. E. sunt comune pentru toate obiectele izomorfe.
În special, izomorfismul păstrează asociativitatea, comutativitatea, distributivitatea.