Chiar și faimosul cuprinde o serie infinită
Și în limitele nelimitate apar,
Deci sufletul imensității locuiește în minuții
Și în limitele cele mai înguste.
Ce bucurie de a discerne minutele din infinit!
Vasta de a percepe în mica, ce divinitate!
Ca și în seria finită infinită sunt cuprinse,
Cât de neîncetat se dovedește a fi limitată,
Deci spiritul imensității trăiește în lucruri mici
Și în granițele cele mai apropiate se află limitele.
Ce bucurie de a discerne cele mai mici în infinit!
Cât de divin să vezi imensitatea în micul!
Jacob Bernoulli. "Arta ipotezelor"

Epitaf și spirală pe mormântul lui Jacob Bernoulli
În 1692, Jacob Bernoulli a arătat primele semne de tuberculoză, din care a murit în 1705. În cinstea lui Iacob și a lui Johann Bernoulli, este numit un crater pe Lună.
El a studiat teoria probabilității din cartea Huygens "Despre calcule într-un joc de noroc", în care încă nu exista o definiție și o noțiune de probabilitate (este înlocuită de numărul de cazuri favorabile). Jacob Bernoulli a introdus o parte semnificativă a conceptelor moderne ale teoriei probabilității și a formulat prima versiune a legii numărului mare. Jacob Bernoulli a pregătit o monografie în acest domeniu, dar nu a reușit să o publice. A fost tipărită postum, în 1713, de către fratele său Nicolae, sub titlul "Arta convingerilor" (Ars conjectandi). Acesta este un tratat cuprinzător asupra teoriei probabilității, statisticilor și aplicării lor practice, rezultatul combinatoricii și al teoriei probabilității secolului al XVII-lea. Numele lui Jacob are o distribuție importantă Bernoulli în teoria probabilităților.
Jacob Bernoulli a publicat, de asemenea, lucrări despre diferite aspecte ale aritmeticii, algebrei, geometriei și fizicii.
Distribuția Bernoulli
Cred că nu există un singur student care să asculte teoria probabilității, care nu ar ști ce este distribuția Bernoulli.
Distribuția lui Bernoulli în teoria probabilităților și statisticile matematice este o distribuție de probabilități discrete care modelează un experiment aleatoriu de natură arbitrară, cu o probabilitate cunoscută de succes sau de eșec.
O variabilă aleatoare X are o distribuție Bernoulli dacă are nevoie doar de două valori: 1 și 0 cu probabilități p și q = 1-p, respectiv. În acest fel:
P (X = 1) = p,
P (X = 0) = q.
Este obișnuit să spunem că evenimentul X = 1 corespunde "succesului", iar X = 0 până la "eșec". Aceste nume sunt condiționate și, în funcție de sarcina specifică, pot fi înlocuite de cele opuse.
Momentele distribuției Bernoulli
E [X] = p,
D [X] = pq.
În general, este ușor de văzut acest lucru
E [X ^ n] = p, pentru orice grad natural n.
Numerele Bernoulli
Numerele Bernoulli reprezintă o secvență de numere raționale "B_0, B_1, B_2". `, considerat prima dată de Jacob Bernoulli în legătură cu calculul sumei de numere naturale consecutive ridicate la același grad:
unde este coeficientul binomial.
proprietăţi
- Toate numerele Bernoulli cu numere impare, cu excepția lui `B_1`, sunt egale cu zero, iar semnele numerelor Bernoulli cu numere paralele se alternează.
- Numerele Bernoulli sunt valorile polinomilor Bernoulli `B_n (x)` pentru `x = 0`:` B_n = B_n (0) `.
Numerele Bernoulli intră adesea în coeficienții de extindere a funcțiilor elementare într-o serie de putere.

Scris în 1713.
Lemniscate Bernoulli
Lemniscata (din latin lemniscatus - "decorat cu panglici") este o curba algebrica plata a ordinului 2n, pentru care produsul distantelor de la fiecare punct la n puncte (foci) este constant.
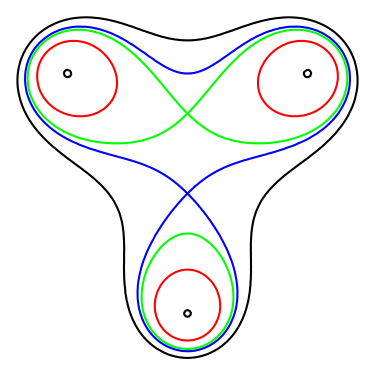
Lemniscate cu trei focare fixe
exemple
- Un lemniscat cu un singur foc (n = 1) este un cerc de rază r, iar cu două focare este un oval Cassini.
- Un caz special al ovalului lui Cassini este lemniscatul Bernoulli, numit după matematicianul elvețian Jacob Bernoulli, care a inițiat studiul lemniscatului.
Lemniscatul Bernoulli este o curbă algebrică plat. Este definit ca locusul punctelor, produsul distanțelor de la care până la două puncte date (foci) este constant și egal cu pătratul de jumătate din distanța dintre focare.
Lemniscatul în formă seamănă cu opt sau cu simbolul infinitului. Momentul în care se traversează lemniscatul se numește punctul nodal sau punctul dublu.

Lemniscate și trucurile ei
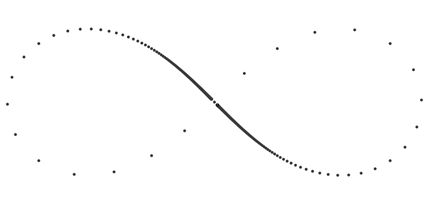
Densitatea punctelor curbei pentru variația uniformă a parametrului
Proprietatea gravitațională a lemniscatelor
Punctul material care se deplasează de-a lungul lemniscatului sub acțiunea unui câmp gravitațional omogen trece prin arc în același timp cu coarda corespunzătoare (a se vedea figura). Se presupune că axa lemniscată face un unghi de 45 ° cu vectorul intensității câmpului, iar centrul lemnului coincide cu poziția inițială a punctului de deplasare.
Construirea unei lemniscate cu ajutorul secantelor
Metode de articulare
Metodă cu balamale