Un grafic al unei funcții diferențiate este considerat a fi convex în jos (în sus) într-un interval dacă este localizat deasupra (de mai jos) orice funcție tangentă pe acest interval.
Punctul graficului unei funcții care separă părțile sale de convexitate diferită se numește punctul de inflexiune.
TEOREM: Dacă funcția are un derivat negativ (pozitiv) secundar în toate punctele intervalului, atunci graficul funcției pe acest interval are convexitatea în sus (în jos).
Exemplul 2. Determinați intervalele de convexitate și punctele de inflexiune ale graficului funcției
Pentru a găsi intervalele de convexitate și punctele de inflexiune, este necesar să găsim al doilea derivat al funcției:
Ecuăm al doilea derivat la zero și rezolvăm ecuația rezultată:
Punctul rezultat împarte axa numerică în două intervale. Definim semnele derivatului secundar pe aceste intervale:
Deoarece punctul aparține graficului și atunci când trece prin acesta al doilea derivat își schimbă semnul, atunci acesta este punctul de inflexiune al graficului funcției.
În intervalul cel de-al doilea derivat ia valori negative, prin urmare, graficul funcției are o convexitate în sus. În consecință, pe interval, graficul funcției are o convexitate în jos.
Ca x → + ∞, x → - ∞ sau în apropierea punctelor de discontinuitate a celui de-al doilea tip, graficul unei funcții poate aborda în mod arbitrar o linie arbitrară. Astfel de linii sunt numite asimptote.
O linie dreaptă se numește asimptota verticală a graficului unei funcții dacă cel puțin una dintre limitele unilaterale ale acestei funcții în punctul a este + ∞ sau -∞.
Se poate observa că pentru a găsi asimptote verticale este suficient să se găsească punctele de discontinuitate ale celui de-al doilea tip. Dacă funcția are un punct de discontinuitate la punctul a. apoi - asimptote verticale.
Asimptota în panta a graficului functiei y = f (x) are forma y = kx + b. unde
.
Rețineți că dacă cel puțin unul dintre coeficienții k sau b este egal cu infinitatea, atunci putem concluziona că nu există asimptote inclinate.
Dacă k = 0. atunci asimptota verticală va fi scrisă sub forma y = b. O astfel de linie este numită asimptot orizontal.
Exemplu 3. Găsiți asimptotele funcției
Este evident că punctul va fi un punct de discontinuitate a celui de-al doilea tip și, prin urmare, linia va fi asimptota verticală a graficului funcției.
Să verificăm dacă funcția are asimptote înclinate:
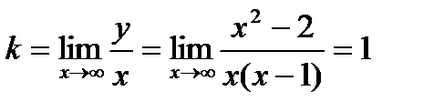
Aceasta înseamnă că linia este o asimptotă oblică a graficului funcției.
Schema generală de cercetare a funcțiilor
1. Găsiți domeniul de definire a funcțiilor.
2. Gasiti punctele de intersectie ale graficului de functii cu axele coordonatelor.
3. Găsiți extrema unei funcții.
4. Găsiți intervale de monotonie.
5. Găsiți punctele de convexitate și inflexiune.
7. Găsiți setul de valori ale funcției
Exemplu 4. Investigați o funcție și construiți graficul acesteia
Vom folosi schema generală pentru a investiga funcția:
1. Este evident că. prin urmare, OOF:
2. Să găsim punctele de intersecție cu axele de coordonate:
. Puncte primite (-; 0); (; 0)
3. Definiți extremele funcției:
x = 1 este punctul maxim (1; 2)
x = 3 este punctul minim (3, 6)
4. Conform schemei de mai sus, concluzionăm că
când funcția crește;
cu scăderea funcției.
Al doilea derivat are valori pozitive la și negativ atunci când. Prin urmare, atunci când graficul funcției are o convexitate în jos și când graficul funcției are o convexă în sus.
Punctul separă părți ale graficului de convexitate diferită, dar din moment ce acest punct nu aparține graficului, acesta nu este un punct de inflexiune. Nu există alte puncte care să separeze părți ale graficului de convexitate diferită. Prin urmare, putem concluziona că nu există nici un punct de inflexiune.
6. Să studiem funcția ca asimptote
Este evident că linia dreaptă este asimptota verticală a graficului funcției.
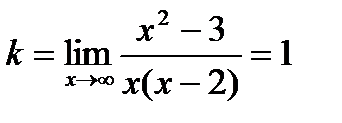
Din punctele găsite, construim un grafic al funcției, precum și graficele asimptotelor.
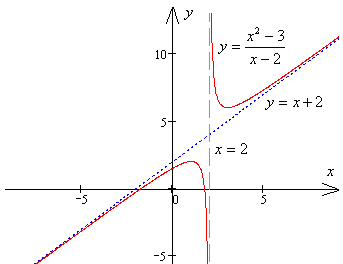
7. Graficul arată că funcția ia toate valorile pe axa numerică, cu excepția intervalului de la maxim la minimul funcției, adică setul de valori ale funcției :.
Funcția F (x) se numește primitivul funcției f (x) pe interval dacă pentru orice x în acest interval este valabil egalitatea F (x) = f (x). Setul tuturor primitivilor funcției f (x) este dat de formula F (x) + C. unde C este un număr constant și se numește un integru indefinit.
Proprietățile integralului nedeterminat:
5) Dacă. atunci. unde este o funcție arbitrar de diferențiat.