Arborele de cod (arborele de codificare Huffman, arborele H) este un arbore binar. în care:
- Frunzele sunt marcate cu simboluri pentru care codificarea este dezvoltată;
- nodurile (inclusiv rădăcina) sunt marcate de suma probabilităților de apariție a tuturor simbolurilor care corespund frunzelor subtreei. a cărei rădăcină este nodul corespunzător.
Metoda Huffman la intrare primește un tabel al frecvențelor apariției simbolurilor în textul sursă. Mai departe, pe baza acestui tabel, arborele de codificare Huffman este construit.
Algoritm pentru construirea unui arbore Huffman.
Pasul 1. Simbolurile alfabetului de intrare formează o listă de noduri libere. Fiecare foaie are o greutate. care poate fi egală fie cu probabilitatea fie cu numărul de apariții ale caracterului din textul comprimabil.
Pasul 2. Sunt selectate două noduri libere ale copacului cu cele mai mici greutăți.
Pasul 3. Creați părinții lor cu o greutate egală cu greutatea lor totală.
Pasul 4. Părintele este adăugat la lista de noduri libere și doi dintre copiii lui sunt eliminați din această listă.
Pasul 5. Un singur arc. ieșirea de la părinte este atribuită biți 1, celălalt bit 0.
Pasul 6. Repetați pașii de la cel de-al doilea, până când rămâne un singur nod liber în lista de noduri libere. El va fi considerat rădăcina copacului.
Există două abordări pentru construirea unui arbore de cod: de la rădăcină la frunze și de la frunze la rădăcină.
Un exemplu de construire a unui arbore de cod. Fie ca secvența inițială de simboluri să fie dată:
Volumul său inițial este de 20 de octeți (160 de biți). În conformitate cu datele prezentate în Fig. 41.1 date (tabelul de apariție a probabilității simbolului, arborele de cod și tabelul de cod prefix optim), secvența originală de caractere codată va arăta astfel:
Prin urmare, volumul său va fi egal cu 42 de biți. Raportul de compresie este de aproximativ 3,8.
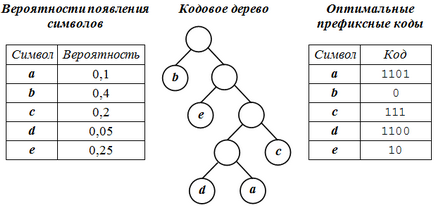
Fig. 41.1. Crearea de coduri prefixe optime
Algoritmul clasic Huffman are un dezavantaj semnificativ. Pentru a restaura conținutul textului comprimat în timpul decodificării, este necesar să cunoaștem tabelul de frecvență utilizat pentru codificare. În consecință, lungimea textului comprimat este mărită de lungimea tabelului de frecvență, care trebuie trimis înaintea datelor, ceea ce poate nega toate eforturile de comprimare a datelor. În plus, necesitatea unei statistici de frecvență completă înainte de a începe codarea reală necesită două treceri pe text: una pentru construirea unui model text (tabelul de frecvență și un arbore Huffman), celălalt pentru codarea reală.
Exemplul 2. Implementarea software-ului algoritmului Huffman folosind un arbore de cod.
Pentru a efectua decodificarea, este necesar să avem un arbore de cod. care trebuie să fie stocate împreună cu datele comprimate. Aceasta duce la o ușoară creștere a cantității de date comprimate. Se utilizează o varietate de formate în care acest arbore este stocat. Să fim atenți la faptul că nodurile arborelui de coduri sunt goale. Uneori, copacul în sine nu este stocat. dar datele inițiale pentru formarea sa, adică informații despre probabilitățile apariției simbolurilor sau a numerelor acestora. Procesul de decodificare este precedat de construirea unui nou arbore de cod, care va fi același ca și pentru codificare.
Termeni-cheie
Comprimarea datelor este un proces care reduce cantitatea de date prin reducerea redundanței.
compresie fără pierderi (complet reversibilă) - este o metodă de comprimare a datelor, în care o porțiune a datelor codificate anterior este restabilită după dezambalare complet fără modificări.
Compresia pierdută este o metodă de comprimare a datelor în care o parte din datele conținute în ea sunt aruncate pentru a asigura comprimarea maximă a matricei originale de date.
Algoritmul comprimării datelor (algoritmul de arhivare) este un algoritm. care elimină redundanța înregistrării datelor.
Alfabetul de cod este setul tuturor simbolurilor fluxului de intrare.
Simbolul de cod este cea mai mică unitate de date care trebuie comprimată.
Un cuvânt de cod este o secvență de simboluri de cod din alfabetul de cod.
Un token este o unitate de date scrise într-un flux comprimat prin algoritmul de compresie.
O expresie este o bucată de date plasată într-un dicționar pentru o utilizare ulterioară în comprimare.
Codificarea este procesul de comprimare a datelor.
Decodificarea este inversul procesului de codificare în care datele sunt restabilite.
Raportul de compresie este o valoare care indică eficiența metodei de comprimare, egală cu raportul dintre dimensiunea fluxului de ieșire și dimensiunea fluxului de intrare.
Raportul de compresie este reciproc al raportului de compresie.
Lungimea medie a unui cuvânt de cod este o valoare care este calculată ca suma ponderată cu probabilitate a lungimilor tuturor cuvintelor de cod.
Metodele statistice sunt metode de comprimare care atribuie codurilor de lungime variabilă simbolurilor fluxului de intrare, cu coduri mai scurte atribuite simbolurilor sau grupurilor de simboluri care au o probabilitate mare de a apărea în fluxul de intrare.
Vocabularul de compresie este o tehnică de compresie care stochează piese de date într-o structură de date numită un dicționar.
Codificarea Huffman (compresie) este o metodă de comprimare care atribuie coduri de lungime variabilă simbolurilor alfabetice pe baza probabilităților de apariție a acestor simboluri.
Un cod de prefix este un cod în care niciun cuvânt de cod nu este un prefix al oricărui alt cuvânt de cod.
Codul prefixului optim este codul de prefix. având o lungime medie minimă.
Arborele de cod (arborele de codificare Huffman, arborele H) este un arbore binar. în care: frunzele sunt marcate cu simboluri pentru care codificarea este dezvoltată; nodurile (inclusiv rădăcina) sunt marcate de suma probabilităților de apariție a tuturor simbolurilor care corespund frunzelor subtreei. a cărei rădăcină este nodul corespunzător.
Rezultatele rezumate
- Comprimarea datelor este un proces care reduce cantitatea de date prin reducerea redundanței.
- Comprimarea datelor poate apărea cu pierderea și fără pierderi.
- Rata de compresie caracterizează gradul de comprimare a datelor.
- Există două modalități principale de compresie: metode statistice și compresie vocabulară.
- Algoritmul lui Huffman se referă la metodele statistice de comprimare a datelor.
- Ideea algoritmului Huffman este aceasta: cunoașterea probabilitatea de apariție a caracterelor în codul sursă, este posibil să se descrie procedura de construire a codurilor de lungime variabilă, constând dintr-un număr întreg de biți.
- Codurile Huffman au un prefix unic, care le permite să decodeze în mod unic, în ciuda lungimii lor variabile.
- Algoritmul Huffman este universal, poate fi folosit pentru a comprima date de orice tip, dar este ineficient pentru fișiere de dimensiuni mici.
- Algoritmul clasic Huffman bazat pe arborele de cod necesită stocarea arborelui de cod, ceea ce sporește gradul de laboriositate al acestuia.