Lucrarea de laborator № 5
Tema: construirea și transformarea graficelor 3D și a altor obiecte voluminoase.
Obiectiv: Pentru a afla funcții complot și diverse obiecte în spațiul definit implicit în formă parametrice, în coordonate polare și coordonate sferice.
Sarcina 1. Construirea grafurilor de funcții în spațiu.
Pentru a construi graficele funcțiilor z = f (x; y) vom folosi funcția Plot3D. Acesta este dat în următoarele forme:
Plot3D [f,<>,<>] - construiește un grafic al funcției z = f (x; y) pentru x variază în intervalul de la;
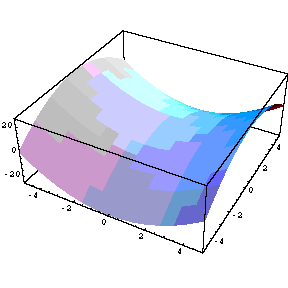
a) Am complot funcția la x variind de la -10 la 10 și la variație de la -10 la 10.
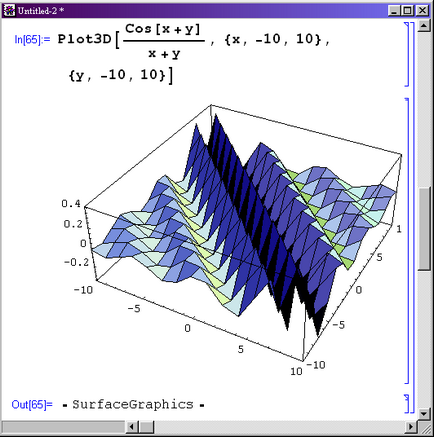
b) Se trasează funcția z = x 2 + y 2 cu x variind de la -10 la 10 și y variind de la -10 la 10.
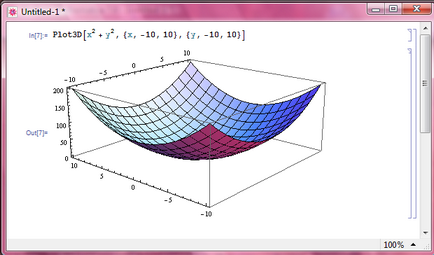
Construiți grafice ale funcțiilor:
; ; . z = sin (xy); x 3 + y 2 - z 2 = 0.
Sarcina 2. Construirea grafurilor funcției în spațiu, dat parametric.
Nu toate suprafețele pot fi definite de ecuația z = f (x, y)) sau tabelar. Este adesea mult mai convenabil să le setați parametric. De asemenea, parametrii pot fi utilizați pentru a specifica curbele în spațiu. Suprafața bidimensională definită parametric sau curbele unidimensionale în spațiul tridimensional pot fi desenate folosind funcția ParametricPlot3D.
Apelează ParametricPlot3D [t. yt. it], min. tmax>] returnează o curbă spațială parametrizată de o variabilă care variază de la tmin la tmax.
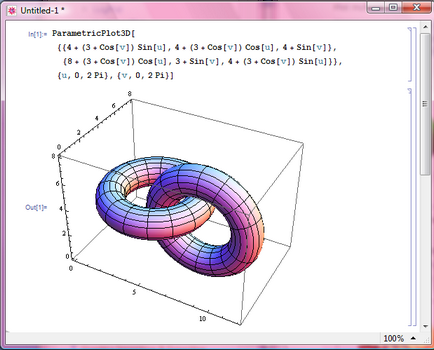
Construiți pe un grafic:
Sarcina 3. Construirea graficii 3D într-un sistem de coordonate sferice.
Aplicarea acestei funcții este cea mai simplă modalitate de a construi o sferă. Acest lucru este normal, deoarece sistemul de coordonate este sferic. Și ce sistem de coordonate se numește sferic?
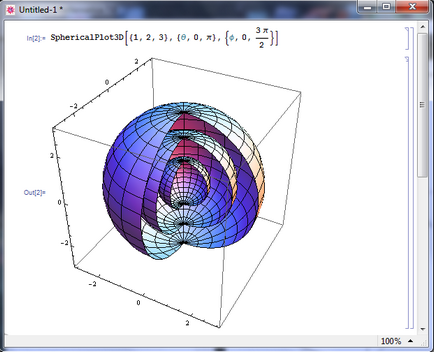
Construiește un grafic de funcții:
a) y = 1+ (Sin (5u) / 5) și v de la 0 la tt, și u de la 0 la 2π;
b) y = 1 + 2Cos (2u), pentru u de la 0 la π, iar pentru v de la 0 la 2π.
Sarcina 4. Figurile de rotație.
Destul de larg răspândite sunt obiectele grafice tridimensionale obținute prin rotirea curbelor în raport cu o anumită axă. De exemplu, transformând un cerc într-un unghi π, puteți obține suprafața mingii. Schimbând limitele modificării unghiului de rotație, se pot construi cifre închise sau neinchise. Pentru a construi astfel de suprafețe (figuri) în Mathematica, utilizați funcția: RevolutionPlot3D [fz, min, tmax>. ] și RevolutionPlot3D [x, fy, fz>, min, tmax>. ].
Construiește un grafic de funcții:
a) z = t 4 - t 2. pentru t de la 0 la 1;
Sarcina 5. Diferite obiecte tridimensionale
Mathematica are un număr de figuri colorate, proiectate ca date de probă (ExampleData). Acestea pot fi folosite pentru a testa funcționarea funcțiilor grafice. În Fig. Figura 5 prezintă construcția unei figuri tridimensionale din exemple utilizând funcția ListSurfacePlot. Numai opțiunea care specifică numărul de fragmente ale formei este utilizată. Celelalte opțiuni sunt setate implicit.
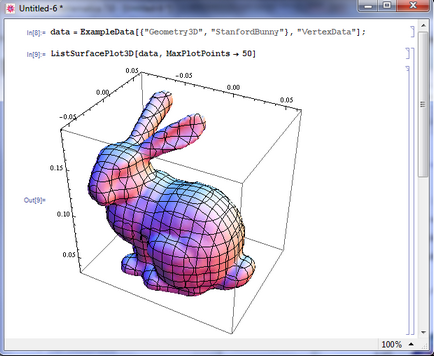
Construiți imaginile așa cum se arată în Fig. 5, pentru:
Sarcina 6. Suprafețe importante ale spațiului (geometria analitică a spațiului).
Pentru a construi grafice în spațiu, funcția familială este deja utilizată. unde f este o funcție a variabilelor x și y, unde. .
Pentru a construi un grafic de suprafață de ordinul doi, trebuie mai întâi să exprimăm variabila z din ecuația canonică. Acest lucru se poate face folosind funcția Solve, care a fost folosită pentru a rezolva ecuațiile, indicând doar variabila z ca variabila necunoscută. De exemplu, exprimăm variabila z din ecuația elipsoidă:
Aceasta înseamnă că construcția unui elipsoid se reduce la construcția într-un sistem de coordonate a două grafice tridimensionale și.
Deoarece graficele trebuie construite într-un sistem de coordonate, folosim funcția Show. În plus, atunci când trasăm grafice pentru a îmbunătăți calitatea graficelor, folosim opțiunea PlotPoints -> n, care indică câte puncte ar trebui să participe la construcție (n este un număr natural). Cu opțiunea Mesh -> False, liniile scheletului de suprafață sunt șterse, ceea ce ajută la ilustrarea vizuală a imaginii.
Fă tu singur exemplul. Modificați parametrii a, b, c și setați modul în care creșterea sau scăderea lor afectează imaginea suprafeței. În acest caz, este necesar să crească sau să scadă intervalul de schimbare a variabilelor.
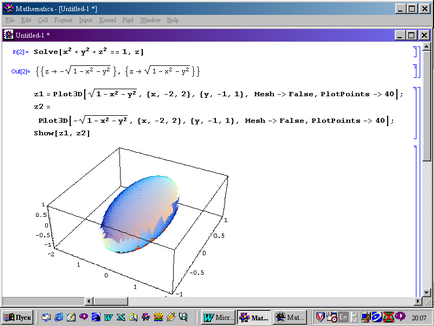
Figura 6 prezintă construcția unui elipsoid dat de ecuație.
b) Hiperboloid cu o singură cavitate.
Figura 7 prezintă construcția unui hiperboloid cu o singură față, dat de o ecuație.
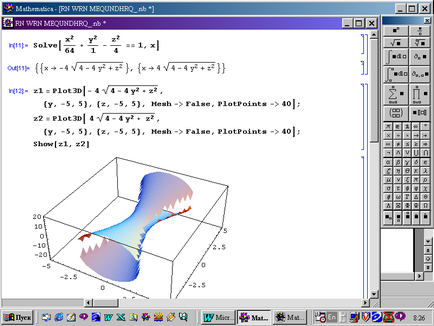
Figura 8 prezintă construirea unui hiperboloid cu două lăzi dat de ecuație.
Construiți următoarele suprafețe secundare:
a) Paraboloidul hiperbolic (ecuația canonică :), dat de ecuație.
b) Un paraboloid eliptic (ecuația canonică :) dat de ecuație
c) Cilindru eliptic (ecuația canonică :), dat de ecuație.
d) Un cilindru hiperbolic (ecuația canonică :) dat de ecuație
e) Un cilindru parabolic (ecuația canonică :) dat de ecuație
f) O pereche de planuri intersectate (ecuația canonică :) dată de ecuație.
g) o pereche de planuri paralele (ecuația canonică:
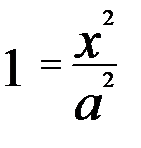
h) O pereche de planuri coincide: ecuația canonică.
Sarcina 7. Schimbați unghiul.
Mathematica oferă utilizatorului posibilitatea de a vizualiza orice figură spațială pe care a construit-o în poziții diferite. Pentru a schimba poziția în spațiul unei forme tridimensionale, utilizați opțiunea 3D View Point Selector. Această opțiune poate fi setată utilizând bara de instrumente Introducere. În acest caz, cursorul trebuie plasat după virgulă și plasat în fața brațului de închidere pătrat.
Figura 9 prezintă un exemplu de utilizare a acestei opțiuni.
Il ilustram diferite poziții ale unui paraboloid hiperbolic în spațiu. În figura 10, acesta este construit fără opțiune, în figura 11 cu aplicația sa.