Sistemul spațial arbitrara a forțelor, precum și un apartament, poate duce la unele centru O și înlocuită cu o singură forță rezultantă și un cuplu cu acest moment. Fundamentarea că echilibrul acestui sistem de forțe este necesară și suficientă pentru a simultan R = 0, și Mo = 0. Cu toate acestea, vectorii pot fi zero numai atunci când toate acestea sunt proiecția zero, pe axa de coordonate, adică. E. Când Rx = = Ry Rz = 0 și Mx = My = Mz = 0 sau atunci când forțele care acționează îndeplinesc condițiile:
Astfel, pentru echilibrul sistemului forței spațiale, este necesar și suficient ca sumele proeminențelor tuturor forțelor sistemului pe fiecare dintre axele de coordonate, precum și suma momentelor tuturor forțelor sistemului în raport cu fiecare dintre aceste axe să dispară.
În cazurile particulare ale unui sistem de forțe convergente sau paralele, aceste ecuații vor fi dependente liniar, iar numai trei dintre cele șase ecuații vor fi independente liniar.
De exemplu, ecuațiile de echilibru ale unui sistem de forțe paralele cu axa Oz. au forma:
Sarcini pentru echilibrul corpului sub acțiunea sistemului de forță spațială.
Principiul de rezolvare a problemelor din această secțiune rămâne același ca și pentru un sistem plan de forțe. După stabilirea echilibrului corpului care va fi luat în considerare, înlocuiți legăturile suprapuse prin reacțiile lor și alcătuiți condițiile de echilibru pentru acest organism, tratându-l drept liber. Ecuațiile obținute determină cantitățile necesare.
Axa este recomandat pentru sisteme mai simple de ecuații pentru a petrece, astfel încât să traverseze mai multe forțe necunoscute sau au fost perpendicular pe ea (dacă este doar complica inutil calcularea proiecții și momente ale altor forțe).
Un element nou în compilarea ecuațiilor este calculul momentelor de forță raportate la axele de coordonate.
În cazurile în care totalul dificil de desen pentru a vedea ce este momentul acestei forțe în raport cu orice axă, este recomandat să se descrie proiecția auxiliară a corpului în desen (împreună cu puterea) într-un plan perpendicular pe această axă.
În cazurile în care calcularea timpului există dificultăți în determinarea proiecția forței pe planul propriu-zis sau umăr această proiecție, se recomandă să se răspândească puterea în două componente reciproc perpendiculare (dintre care una este paralelă cu orice axă de coordonate), și apoi folosește teorema lui Varignon lui.
Exemplul 5. Cadrul AB (Fig.45) este menținut în echilibru de articulația A și de tija BC. La marginea cadrului este o greutate de P. Determinați reacția balamalei și forța din tija.
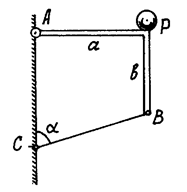
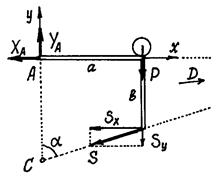
Considerăm echilibrul cadrului împreună cu sarcina.
Construim o schemă de calcul, arătând cadrul drept un corp liber și arătând toate forțele care acționează asupra lui: reacțiile de legătură și greutatea sarcinii P. Aceste forțe formează un sistem de forțe situate în mod arbitrar în plan.
Este de dorit să compilați astfel de ecuații, astfel încât în fiecare să existe o forță necunoscută.
Se recomandă să se compună ecuațiile de momente cu privire la trei puncte, punctele de intersecție a liniilor de acțiune ale forțelor necunoscute.
În problema noastră, acesta este punctul lui A. unde necunoscuții și; punctul C. unde liniile de acțiune ale forțelor necunoscute se intersectează; punctul D este punctul de intersecție a liniilor de acțiune ale forțelor u. Vom compune ecuația proiecțiilor forțelor pe axa y (pe axa x este imposibil de proiectat, deoarece este perpendicular pe linia dreaptă AC).
Și, înainte de a face ecuațiile, facem o remarcă mai utilă. Dacă există o forță asupra schemei de proiectare care este localizată astfel încât brațul ei nu este ușor, atunci pentru a determina momentul este recomandat să se descompună mai întâi vectorul acestei forțe în două, mai bine direcționate. În această problemă, descompunem forța în două: și (figura 37) astfel încât modulele lor
Din a doua ecuație găsim:
Din moment ce a fost S <0, то стержень ВС будет сжат.
Exemplul 6. Un raft dreptunghiular de greutate P este ținut într-o poziție orizontală de două tije CE și CD. atașat la perete la punctul E. Tije de aceeași lungime, AB = 2a. EO = a. Definiți forțele din tije și reacțiile buclelor A și B.
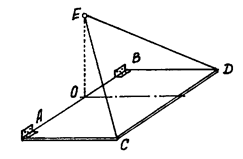
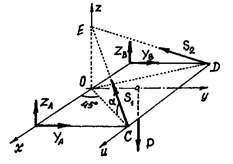
Considerăm echilibrul plăcii. Construim schema de calcul (Fig.46). Reacția buclelor este indicată de obicei de două forțe perpendiculare pe axa buclei :.
Forțele formează un sistem de forțe situate în mod arbitrar în spațiu. Putem compune 6 ecuații. Necunoscut - și șase.
Ce ecuații trebuie compuse - este necesar să gândim. Este de dorit ca ele să fie mai simple și să conțină mai puține necunoscute.
Să compunem următoarele ecuații:
Din ecuația (1) obținem: S1 = S2. Apoi din (4) :.
Din (3): YA = YB și, conform (5) ,. De aici Din ecuația (6), deoarece S1 = S2. urmează ZA = ZB. Apoi, prin (2), ZA = ZB = P / 4.
Din triunghiul. în cazul în care. urmează.
Prin urmare, YA = YB = 0,25P, ZA = ZB 0,25P.
Pentru a testa soluția, se poate elabora o altă ecuație și se poate vedea dacă este mulțumită de valorile găsite ale reacțiilor:
Problema este rezolvată corect.