Pentru a descrie schemele obținute prin combinarea diferitelor porți, aveți nevoie de un tip special de algebră în care toate variabilele și funcțiile pot lua doar două valori: 0 și 1. O astfel de algebră se numește booleană. Este numit după matematicianul englez George Boole (1815-1864). De fapt, în acest caz, este vorba despre un tip special de algebrei booleene, și anume - despre algebra circuitelor releu, dar termenul „algebra booleană“ este adesea folosit pentru a însemna „circuite releu algebra“, deci nu vom distinge între ele.
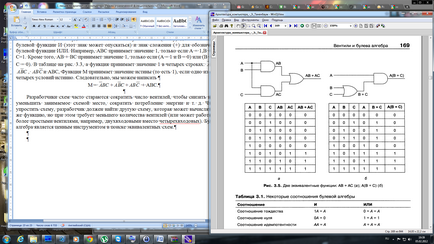
Ca și în algebra obișnuită (adică în cea studiată în școală), algebra booleană are propriile funcții. O funcție booleană la intrare primește una sau mai multe variabile și iese un rezultat care depinde numai de valorile acestor variabile. Se poate defini o funcție simplă F prin a spune că F (A) = 1 dacă A = 0 și F (A) = 0 dacă A = 1. O astfel de funcție este o funcție a HE (vezi Fig.
Deoarece funcția booleană a variabilelor n are doar 2n posibil combinații de valori ale variabilelor, această funcție poate fi descrisă complet într-un tabel cu rânduri 2n. Fiecare linie va da valoarea funcției pentru diferite combinații de valori variabile. Un astfel de tabel este numit tabelul de adevăr. Toate tabelele din Fig. 3.2 sunt tabelele de adevăr.
Dacă suntem de acord întotdeauna avem tabelul de linii de adevăr, în ordine numerică, adică pentru cele două variabile în ordinea 00, 01, 10, numărul binar 2n-biți 11, funcția poate fi descrisă complet, care este obținut prin citirea rezultatelor coloana verticală din tabelul de adevăr . Astfel, NAND - o 1110 NOR - 1000 și - 0001 și OR - 0111. Este clar că există doar 16 funcții booleene de două variabile, care corespund la cele 16 posibile siruri de 4 biți. În algebra obișnuită, dimpotrivă, există un număr infinit de funcții de două variabile, precum și oricare dintre ele nu poate fi descrisă prin furnizarea unui tabel de valori ale acestei funcții pentru toate valorile posibile ale variabilelor de intrare, deoarece fiecare variabilă poate lua un număr infinit de valori.
În Fig. 3.3, este prezentată tabelul de adevăr pentru o funcție booleană a trei variabile: M = F (A, B, C). Această funcție majoritate care are valoarea 0 în cazul în care cele mai multe dintre variabilele sunt egale cu 0 sau 1, în cazul în care cele mai multe variabile egale cu 1. Cu toate că orice funcție booleană poate fi determinată folosind tabelul de adevăr, odată cu creșterea numărului de variabile astfel de tip de înregistrare devine greoaie. Prin urmare, în locul tabelelor de adevăr, este adesea folosită o altă versiune a înregistrării.
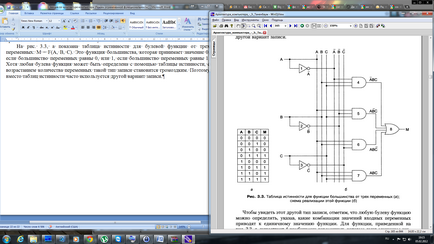
Pentru a vedea acest alt tip de înregistrare, rețineți că orice funcție booleană poate fi determinată prin specificarea combinațiilor de valori ale variabilelor de intrare care conduc la o singură valoare a funcției. Pentru funcția prezentată în Fig. 3.3, a, există 4 combinații de variabile care dau valoarea unitară a funcției. Vom desena o linie deasupra variabilei, indicând faptul că valoarea sa este inversată. Absența unei bare înseamnă că valoarea variabilei nu este inversată.
În plus, vom folosi semnul de multiplicare (punct) pentru a desemna funcția Boolean AND (acest semn poate fi omis) și semnul adițional (+) pentru a indica funcția Boolean OR. De exemplu, ABC ia valoarea 1 numai dacă A = 1, B = 0 și C = 1. În plus, AB + BC ia valoarea 1 doar dacă (A = 1 și B = 0) sau (B = 1 și C = 0). În tabelul din Fig. 3.3, iar funcția are valoarea 1 în patru rânduri:
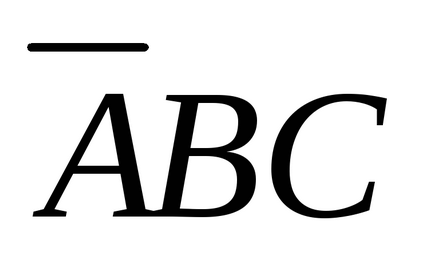
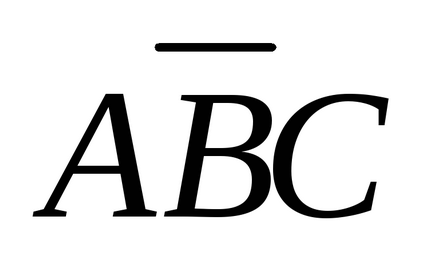
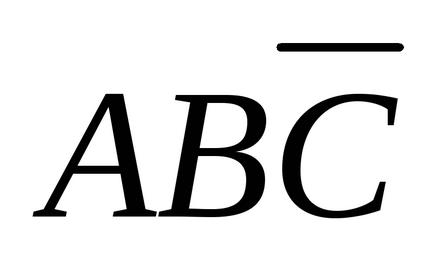
scheme dezvoltatorii încearcă adesea să reducă numărul de porți pentru a reduce prețul, reduc ocupat schema site-ului, reduce consumul de energie și așa mai departe. d. Pentru a simplifica sistemul, dezvoltatorul trebuie să găsească un alt circuit care poate calcula aceeași funcție, dar este nevoie de un număr mai mic de porți ( sau poate funcționa cu porți mai simple, de exemplu, cu două intrări în loc de porți cu patru intrări). Boolean algebra este un instrument valoros în căutarea circuitelor echivalente.