Baza unui triunghi isoscel este egală cu 12
 Bună ziua!
Bună ziua!
Astăzi vom examina problema din cursul clasei a VIII-a, care va fi utilă și pentru absolvenții actuali
Clasa 9.
Toate deoarece folosesc formule pentru a determina
Zona triunghiului prin razele cercurilor inscripționate și circumscrise.

obiectiv:
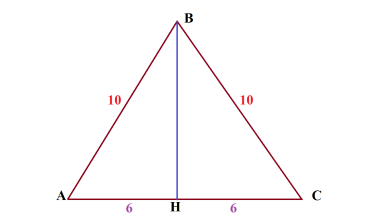
Baza unui triunghi isoscel este de 12 cm, iar partea laterală este de 10 cm. Găsiți razele inscripționate în triunghi și împrejurul circumcizilor circumscris unui triunghi!
Soluție: Lăsăm HV perpendiculară din vârf
triunghiul B pe baza difuzorului.
Știm că această perpendiculară este simultan un bisector și o mediană a unui triunghi isoscel. Ie AN = CH = 6 cm.
Din triunghiul drept ABN, cunoscând hypotenuse, AB = 10cm,
și cateterul AH = 6 cm, găsim al doilea picior al VN.
Prin teorema lui Pythagorean, BH = √ (10² - 6²) = √64 = 8.
Prin urmare, aria triunghiului ABC poate fi calculată din formula
S = 1/2 * AC * BH = 1/2 * 12 * 8 = 48 cm².
În același timp, aria triunghiului poate fi calculată din formula S = pr,
unde p este jumătatea perimetrului triunghiului, p = (10 + 10 + 12) / 2 = 16
r este raza cercului înscris.
Avem: pr = 48 ⇒ r = 48 / p = 48/16 = 3 cm.
Zona triunghiului prin produsul laturilor
iar raza cercului circumscris poate fi exprimată după cum urmează:
S = abc / 4R, unde
a, c, c - partea triunghiului,
R este raza cercului circumscris.
Zona triunghiului pe care o cunoaștem, lungimea laturilor, de asemenea,
putem găsi raza.
48 = 10 * 10 * 12 / 4R ⇒
R = 10 * 10 * 12/4 * 48 = 6,25 cm.
Raspuns: Raza cercului inscris este de 3 cm,
raza cercului circumscris este de 6,25 cm.
Asta e tot pentru ziua de azi. Succesuri și noi provocări!
Veți fi, de asemenea, interesat de:
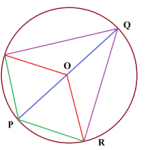
- Un diametru și două coarde sunt trase prin punctul P al cercului
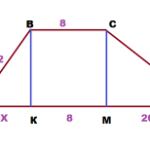
- Înălțimea trapezului prin bazele 8 și 28
- Exemple de clasă de geometrie 7.
