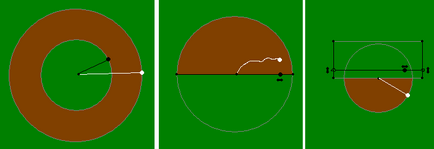
Caprele sunt animale foarte foame. Ei mănâncă toată iarba pe care o pot atinge. Prin urmare, ele sunt ținute pe o lesă. 1. Legați capra la pajiște pentru a mânca cercul.
Răspuns. Trebuie să-l legați cu o funie, lungimea căreia este egală cu raza cercului, de cuibul care stă în centrul său. Apoi, pentru a merge dincolo de cercul, capra nu este suficient de lungimea cablului, astfel încât toate punctele din afara cercului scos din centru la o distanță mai mare decât raza (și, prin urmare, decât lungimea cablului). În schimb, toate punctele cercului sunt situate la o distanță mai mare de centrul său decât raza sa, astfel încât capra poate mânca tot ce este în interiorul cercului.
2. Ce site va mânca capra dacă este legată între două picioare? (Cablul este legat de două picioare și tras printr-un guler de capră.)
Răspuns. Ea va mânca exact o bucată, ale cărei capete sunt cuiburi. Să dovedim că este așa. Într-adevăr, iarba din orice punct al acestui segment, poate mânca; dacă ar putea mânca mai iarbă în orice punct care nu se află în acest interval, coarda pentru care este atașat, ar trebui să se aplece în spate, dar cu condiția problemei este întinsă, astfel încât nicăieri altundeva pentru a obține capra nu se poate.
3. Rodion se plimba pe lunca, tinand o capra pe o lungime de 1m lungime. Traseul său are forma unui dreptunghi cu laturile 3 și 5 m. Ce parte din luncă mănâncă capra?
Notă. Dacă nu puteți rezolva imediat această problemă, încercați să decideți restul, apoi reveniți la ea. De asemenea, este recomandat să faceți același lucru în toate celelalte cazuri.
Instrucțiune 2. Rezolvați problema numărul 5 în primul rând.
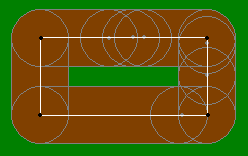
Răspuns. În raza cercului în jurul 1m orice punct de fiecare parte a dreptunghiului toate mâncată (figura ilustrează exemple ale unor astfel de cercuri). Exterioare Formele de delimitare vor fi dintr-un dreptunghi cu colțuri rotunjite (uita la desen mai aproape ați înțeles de ce raza de curbură este egală cu 1 m) și părțile laterale 3 + 1 + 1 = 5 și 5 + 1 + 1 = 7 metri. Limita interioara este deja un dreptunghi obisnuit cu laturile 3 - 1 - 1 = 1 si 5 - 1 - 1 = 3 metri.
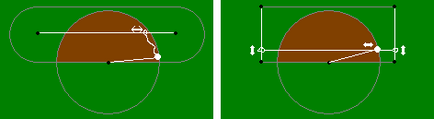
4. Legați o capră cu frânghii și cârlige pentru a putea mânca iarbă numai în interiorul unei secțiuni de această formă:
Răspuns. Această zonă este intersecția a două cercuri. Împărțiți capul ca în prima sarcină, astfel încât să nu poată ieși din primul cerc, în centrul primului cerc pe o frânghie, lungimea căreia este egală cu raza acestui cerc. În același timp, legăm capra cu o altă coardă, a cărei lungime este egală cu raza celui de-al doilea cerc, până la centrul acestui cerc. Ca urmare, capra nu poate părăsi primul cerc, deoarece este legat de centrul său și de cel de-al doilea cerc, deoarece este de asemenea legat de centrul său. Adică, va fi mereu în intersecția acestor două cercuri. (Definiția și desenul intersecției seturilor pot fi găsite aici).
Notă: în general, la capra nu a venit de la intersecția oricare două seturi, suficient (deși nu neapărat, de fapt, poate fi o modalitate de a realiza acest lucru într-un mod diferit), să-l lega, astfel încât să nu iese din prima, și să nu iasă din al doilea , adică rezolvarea a două probleme independente.
5. Trageți coarda între cele două picioare în luncă. La cea de-a doua coardă legăm un capăt la gulerul caprei, iar pe a doua vom face o buclă care alunecă liber de-a lungul coardei. Care site va mânca capra?
Răspuns. La o distanță egală cu lungimea celei de-a doua coarde, din fiecare punct al primei funii, totul va fi mâncat. Astfel, cercurile ale căror centre se află pe intervalul dintre cele două picioare (figura prezintă exemple de mai multe astfel de cercuri) vor fi consumate. Formele lor unire o formă care constă dintr-un dreptunghi și două semicercuri (poate fi numit și un dreptunghi cu colțuri rotunjite a căror rază de rotunjire este egală cu lățimea dreptunghiului și lungimea celei de a doua coarda, și un dreptunghi egal ca lungime prima coarda plus dublul lungimii celei de a doua coarda).
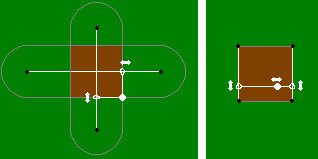
6. Țineți capra cu frânghii și cuie
a) într-un semicerc;
b) în pătrat;
c) într-un dreptunghi (pentru un dreptunghi rezolvat în două moduri diferite).
Notă. Imaginați-vă fiecare dintre aceste figuri ca intersecția a două figuri pentru care o sarcină similară a fost deja rezolvată mai devreme. În plus, pentru un pătrat și un dreptunghi, puteți găsi o altă soluție.
a) Mai întâi legăm capra, astfel încât să nu iasă din cerc. Trebuie să adăugați mai multe frânghii pentru ao păstra în jumătatea dreaptă. Această parte a limitei semicirclei este un segment de linie dreaptă și am avut o astfel de limită înainte de problema 5. Prin urmare, o legăm suplimentar în același mod ca și în acea problemă. Deci, este posibil să se reprezinte un semicerc ca intersecția unui cerc și cifra obținută în problema 5. De asemenea, puteți înlocui figura 5 cu un dreptunghi.
b) Un pătrat este intersecția a două figuri din Problema 5, pentru care lungimea celor două corzi este aceeași.
c) Dreptunghiul poate fi, de asemenea, reprezentat ca intersecția a două astfel de piese, dar puteți veni cu un alt sistem de frânghie în cazul în care o frânghie va aluneca cu balamale pe două șine, iar capra este legat de ea de guler, astfel încât el ar putea merge de-a lungul frânghiei.
Următoarele sarcini implică câini. Ei intervin cu capra: capra nu merge acolo unde câinele poate ajunge. Dar pentru ca caprele să nu fie foame, câinii sunt de asemenea păstrați pe o leșie. 7. Cu ajutorul unui câine, păstrați capra
a) în inel;
b) într-un semicerc.
Fie A zona accesibilă caprei fără a lua în considerare câinii, B - zonele accesibile câinilor. Apoi observăm că capra nu a putut ieși din diferența multimii A \ B (prin definiție, un punct aparține A \ B, dacă și numai dacă aparține A, dar nu face parte din B, care este exact aceeași definiție de pași de câine pe capră).
a) Inelul este diferența a două cercuri având același centru. Deci, capra trebuie să fie legată astfel încât să meargă în jurul unui cerc mai mare, iar câinele - pe cel mai mic.
b) jumătate de cerc poate fi reprezentat ca diferență între un cerc și un dreptunghi sau un cerc și dau seama de problema 5. Este posibil pentru a rezolva această problemă, oricum, lasa cainele intins de-a lungul diametrul unui cerc de frânghie și împărțind astfel cercul în două părți diferite. Apoi capra nu va putea să se deplaseze într-o altă parte a cercului și să rămână în semicercul unde era inițial. (De altfel, acest exemplu arată că capra nu este neapărat să meargă peste diferența stabilită, care în acest caz reprezintă întreaga gamă fără segment, deoarece este împărțit într-un număr de părți care nu au legătură.)