2. PROIECȚII ORTOGONALE ALE PUNCTULUI
Poziția unui punct în spațiu este determinată de coordonatele (x, y, z) care arată distanțele la care punctul este îndepărtat din planurile de proiecție (figura 2.1).
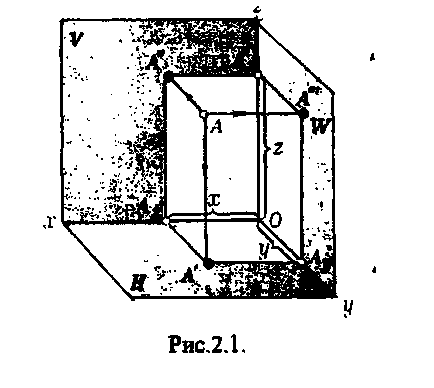
Pentru a determina distanța, este de ajuns prin punctul A pentru a efectua direct, perpendicular pe planurile proeminentelor definesc punctul A“, A“, A '“satisfacerea acestor linii cu planul de proiecție și a valorilor măsurate ale intervalelor [AA«], [AA»3, [AA "], care va indica, respectiv, valorile solicitanților z, ordonate y și abscise x din punctul A.
Punctele A ', A ", A" sunt numite proiecțiile ortogonale ale punctului A și conform notei acceptate:
A 'este proiecția orizontală a punctului A;
A "este proiecția frontală a punctului A;
A "este proiecția profilului de la punctul A.
Liniile drepte (AA '), (AA "), (AA'") sunt numite proiectând grinzi drepte sau proiectate.
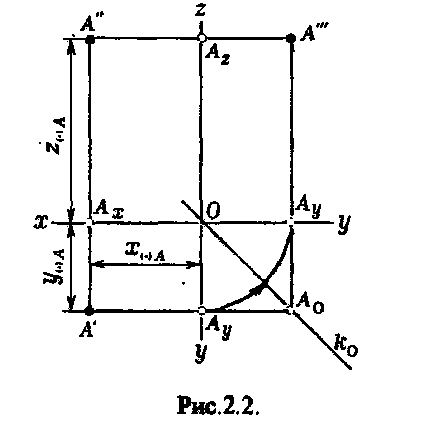
Diagrama punctului A, prezentată în Fig.2.2. poartă aceleași informații ca și aspectul spațial. Proiecția orizontală a punctului A este determinată de coordonatele x, y. distanța de la punctul A la planurile W și V.
Proiecția frontală a punctului A este determinată de coordonatele x și z, adică distanța de la A floW și H.
Proiecția profilului punctului A este determinată de coordonatele y și z, adică distanta de V si N.
A
Poziția unui punct în spațiu poate fi determinată dacă sunt date cel puțin două coordonate. Cunoscând direcția pentru valorile pozitive și negative ale axelor de coordonate, determinați afinitatea punctului pentru oricare dintre cei opt octanti. Pentru aceasta, puteți compila tabelul următor:
3. PROIECTE ORTOGONALE DIRECT
O linie dreaptă este definită de două puncte pentru a construi o diagramă dreaptă, este necesar să se construiască proiecțiile a numai două puncte.
O linie dreaptă în spațiu poate fi dispusă în moduri diferite față de planurile proiecțiilor. Directă, nu paralelă și nu perpendiculară pe oricare dintre planurile proiecțiilor, se numește poziția generală directă.
3.1. Urme ale unei linii drepte
O linie de poziție generală intersectează toate cele trei planuri de proiecție.
Punctul de intersecție (întâlnire) al unei linii drepte cu planul de proiecție se numește linia dreaptă. Punctul de intersecție al liniei 1 cu planul orizontal al proiecțiilor se numește urme orizontale ale liniei drepte lh. cu o linie frontală a liniei drepte lv. cu o linie profil - profil a liniei drepte lw (figura 3.1).
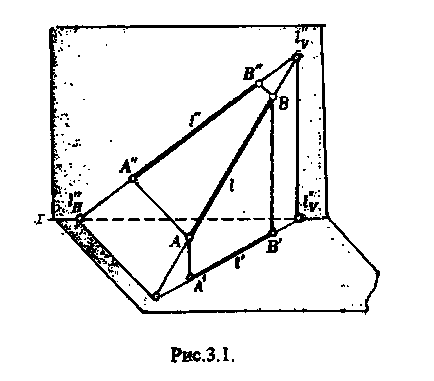
H , 1 H“, 1 H , lv“, lv“, lv“, LW“, lw“, lw“„- respectiv orizontal, frontal, profilul de proiecție urme 1H LV lw Evident, 1H“... = LH ", lv" = lv Lw "" = lW.
Pentru a trasa o urmă orizontală a liniei 1 în figura 3.2, trebuie să continuăm proiecția frontală a liniei 1 la intersecția cu axa x la punctul 1 ", apoi, folosind principiul apartenenței la punctul liniei drepte, să terminăm construcția lui 1H '.
Pentru a construi o linie frontală a liniei 1, este necesar să se extindă proiecția orizontală a liniei drepte 1 la intersecția cu axa x în punctul lv 'și să se completeze liniile corespunzătoare de comunicare lV ".
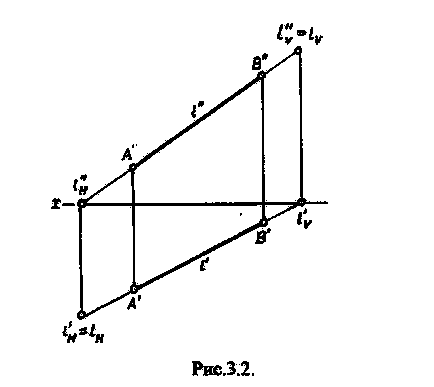
Construit profilat în mod similar, linia de cale 1. În acest scop, fie în continuare linia de proiecție frontală I la intersecția cu axa z în punctul LW“, fie o proiecție orizontală a axei 1 la punctul y intersecție din LW„și linii de comunicație respective fiind terminat de proiecție lipsește.
3.2. Situații private directe
O linie dreaptă poate ocupa o poziție privată cu privire la planurile de proiecții:
a) paralel cu planul de proiecție;
b) perpendicular pe planul proiecției;
c) aparținând planului de proiecție.
3.2.1. Niveluri directe
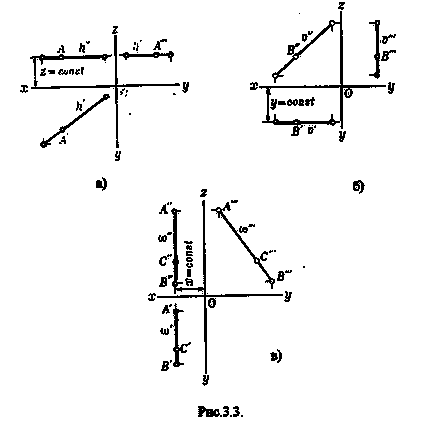
Liniile drepte paralele cu planul proiecțiilor sunt numite linii drepte (Fig.3.3).
Orizontul este o linie dreaptă paralelă cu planul orizontal al proeminențelor (Fig.3.3.a.).
Frontal-drept, paralel cu planul frontal al proiecțiilor (Fig.3.3.b.).
Linia dreaptă a profilului este o linie dreaptă paralelă cu planul profilului proeminențelor (Fig.3.3.c).
3.2.2. Proiectarea liniilor drepte
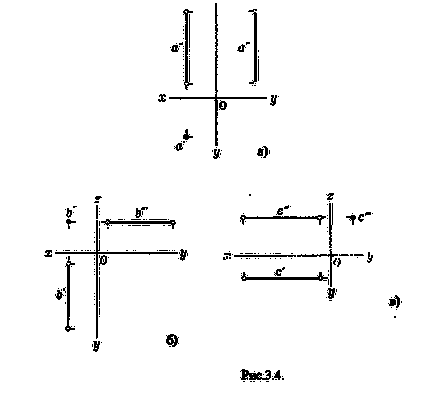
Liniile drepte perpendiculare pe orice plan de proiecție sunt numite linii de proiectare (Fig.3.4).
Liniile drepte perpendiculare pe planul orizontal al proiecțiilor sunt numite linii drepte care se proiectează pe orizontală (figura 3a).
Liniile drepte perpendiculare pe planul de proiecție frontală sunt numite linii de proiectare frontală (figura 3.4.6)
Liniile drepte, perpendiculare pe planul profilului proiecțiilor, se numesc linii de proiectare a profilului (figura 3.4b).
3.2.3. Liniile drepte aparținând planului proiecției
Acesta este un caz special de niveluri directe.
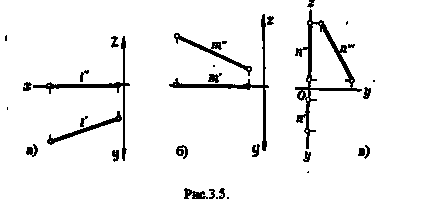
O caracteristică caracteristică a acestor linii este apartenența a două proiecții la axele de coordonate directe. În Fig.3.5. arată liniile de proiecție 1, m, n. 1 parte orizontală de proiecție (ris.3.5.a.) m -fron plane Direct liniar tal proiecție (ris.3.5.b.) n -profilnoy plan de proiecție directă (Fig. 3. 5v).
3
Liniile drepte în spațiu pot ocupa o poziție reciprocă diferită: pot fi paralele, se intersectează și se intersectează.
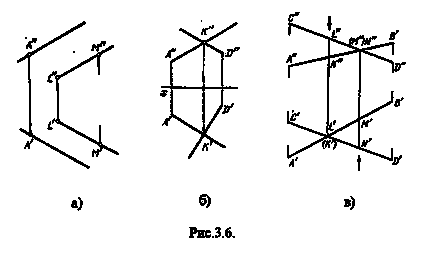
Dacă liniile din spațiu sunt paralele, atunci proiecțiile lor cu același nume sunt paralele (figura 3a). Converse este, de asemenea, adevărat.
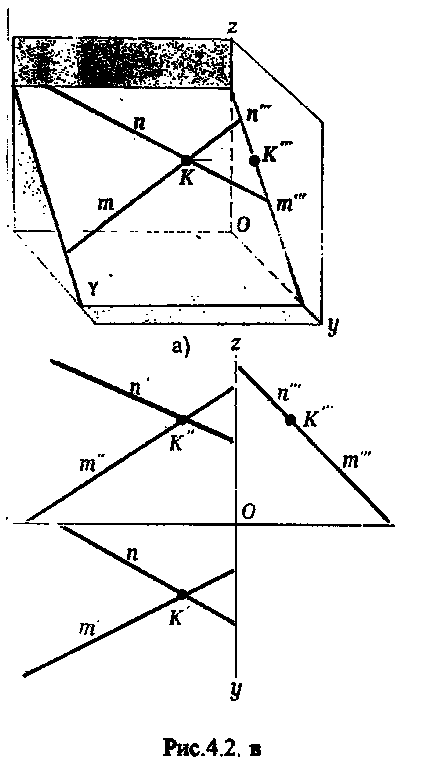
Dacă liniile se intersectează în spațiu, atunci proiecțiile lor cu același nume se intersectează în desen. În acest caz, punctele de intersecție ale proeminențelor acestor linii se află pe o linie de comunicație (figura 3.6b).
Dacă liniile din spațiu se intersectează, atunci în desen se pot intersecta proiecțiile lor cu același nume, dar punctele de intersecție ale acestor proiecții nu se află pe aceeași legătură (fig.3b).
T
4. Determinarea dimensiunii naturale a unui segment
metoda unui triunghi drept
Liniile drepte de poziție generală pe oricare dintre planurile proiecțiilor nu sunt proiectate în dimensiune completă (HB).
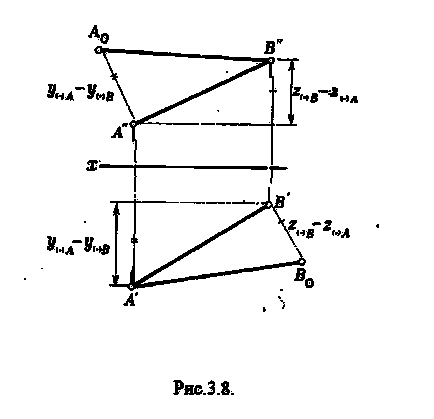
Valoarea aturalnaya poziția generală interval este ipotenuza unui triunghi dreptunghic cu cateta din care este proiecția segmentului pe unul dintre planurile de proiecție, iar celelalte capete ale diferenței interval de distanțe față de același plan (Figura 3.7.).
Din figura 3.7. se vede că unghiul de înclinare a unei linii drepte la planul proeminențelor este definit ca un unghi format de o linie dreaptă cu proeminența sa pe acest plan. Acest unghi intră și în triunghiul drept, care este construit pentru a determina segmentul HB al segmentului (figura 3.8). Astfel, unghiul dintre piciorul de proiecție și hypotenuse al unui triunghi drept este egal cu valoarea reală a unghiului de înclinare al segmentului față de planul proiecțiilor pe care sunt construite construcțiile.
4. PROIECȚII ORTOGONALE ALE PLANULUI
4.1. Metode pentru specificarea unui plan într-un desen
În desen, planul poate fi specificat în următoarele moduri:
- proiecții a trei puncte care nu aparțin aceleiași linii;
- proiecții unei linii drepte și un punct care nu îi aparține;
- proiecții de linii intersectate;
- proiecții de linii paralele;
- proiecții unei figuri geometrice plate;
4.2. Urme ale avionului
Linia dreaptă de-a lungul căreia planul intersectează planul proiecțiilor se numește linia plană (figura 4.1).
În acest caz, distingeți:
-traseul orizontal este o linie dreaptă de-a lungul căreia planul intersectează planul orizontal al proeminențelor H (n);
-Traiectul din față este o linie dreaptă de-a lungul căreia planul intersectează planul frontal al proeminențelor V (v);
-
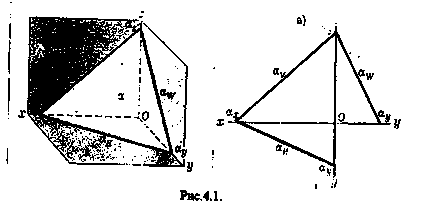
ochelarii în care se intersectează două piese sunt numite urmele de urme.
Pentru a construi urme ale planului, este necesar să găsim urmele a două linii drepte arbitrare ce aparțin acestui plan.
Un plan care nu este paralel și nu este perpendicular pe niciuna dintre planurile de proiecție este denumit un plan general de poziție.
4.3 Planurile unei anumite poziții
Avioanele plană paralele sau perpendiculare pe orice plan de proiecție sunt numite planuri de o anumită poziție.
4.3.1. Proiecte de avion
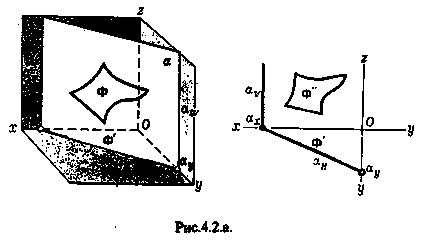
Planurile plane perpendiculare pe planurile de proiecție sunt numite proeminente (figura 4.2).
Un plan perpendicular pe planul orizontal al proiecțiilor se numește proeminență orizontală (Fig.4.2.a.).
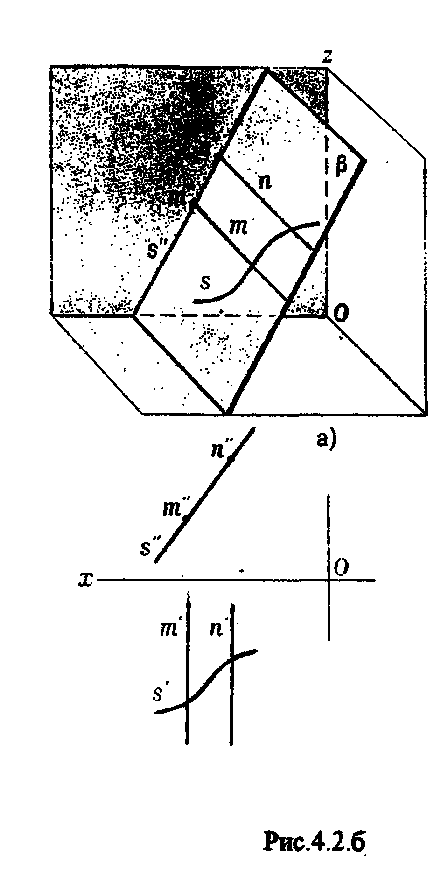
Planul perpendicular pe planul frontal al proiecțiilor se numește proiecția frontală (figura 4.2.6).
Un plan perpendicular pe planul profilului proeminențelor se numește profil-proiecție (figura 4.2.c).