Un model de computer ilustrează particularitățile mișcării moleculelor. Sunt luate în considerare moleculele monoatomice, diatomice și triatomice, se introduce noțiunea de "grad de libertate".
Numărul de grade de libertate a unui obiect material este numărul de coordonate independente care trebuie specificate pentru a determina în mod unic poziția acestui obiect față de cadrul de referință în cauză.
De exemplu, poziția unui punct material în spațiu este determinată de trei coordonate x. y. z. în consecință, punctul material are trei grade de libertate.
Două puncte materiale, situate la o distanță neschimbată una de cealaltă (de exemplu, un model al unei molecule diatomice cu o legătură rigidă între atomi), au cinci grade de libertate - trei de translație și două de rotație. Astfel, o moleculă diatomică poate efectua cinci mișcări independente: trei mișcări de translație de-a lungul axelor X.Y. Z și două rotații relative la axele X și Y (figura 1). Experiența arată că rotirea în jurul axei Z pe care se află centrele ambilor atomi poate fi excitată numai la temperaturi foarte ridicate. La temperaturi obișnuite, nu se produce rotirea în jurul axei Z, așa cum nu se rotește o moleculă monatomică.
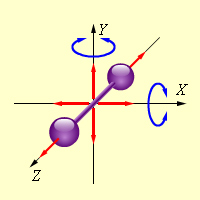
Fiecare mișcare independentă se numește gradul de libertate. Astfel, o moleculă monatomică are 3 grade de libertate de translație, o moleculă diatomică "rigidă" are 5 grade (3 translaționale și 2 rotaționale), iar o moleculă poliatomică are 6 grade libertate (3 translaționale și 3 rotații).
La temperaturi suficient de ridicate, grade de libertate suplimentare de libertate sunt excitate în moleculele poliatomice asociate cu o schimbare în distanțele dintre atomi. De exemplu, într-o moleculă diatomică în condiții date, există 6 grade de libertate (3 translaționale, 2 rotaționale și 1 vibraționale).
Dacă se ia în considerare și gradele de libertate ale vibrațiilor, atunci pentru fiecare grad vibrațional de libertate a moleculei, energia cinetică medie este kT. deoarece mișcarea vibrațională este asociată cu prezența nu numai a energiei cinetice, ci și a energiei potențiale, iar pentru oscilațiile mici (armonice), valoarea medie a energiei potențiale este egală cu valoarea medie a energiei cinetice. Prin urmare, pentru fiecare grad de libertate vibrațional este necesar:
Modelul poate fi utilizat în modul de comutare manuală a cadrelor și în modul de demonstrare automată (Film).