Metoda este orientată spre rezolvarea problemelor cu funcții obiective patratice și se bazează pe rezultate teoretice fundamentale. Deși utilizate în situații reale, algoritmii sunt eficiente pentru funcții obiectiv pătratice să nu funcționeze bine cu mai complexe funcții obiective, cu toate acestea, această abordare pare a fi destul de rezonabil.
Definiția. lăsa


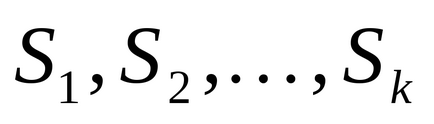


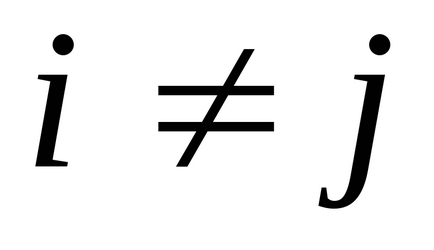
Un exemplu. Luați în considerare funcția
.
Ca matrice

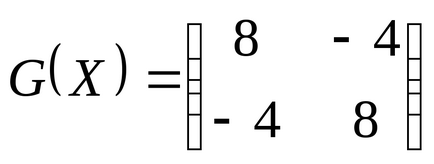
Ca una din direcțiile pe care le alegem
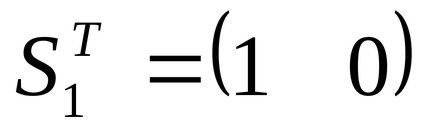
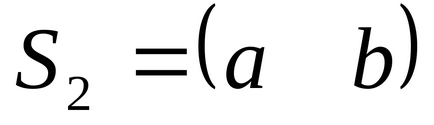
.
Trebuie remarcat faptul că direcțiile conjugate sunt alese ambiguu. Cu toate acestea, dacă adăugăm condiția de normalizare, atunci le putem defini fără ambiguitate:
.
Aprobarea. Orice functie patratica
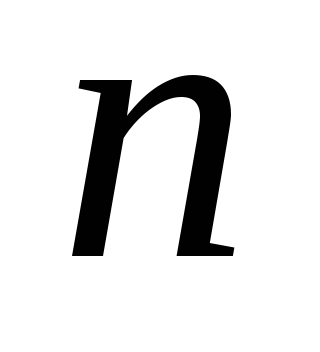
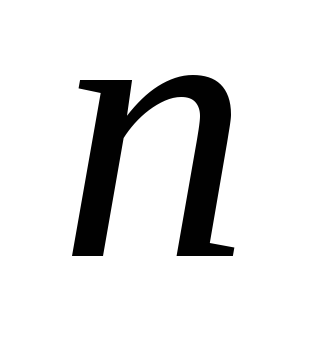
O funcție arbitrară poate fi reprezentată destul de bine în vecinătatea punctului optim prin aproximarea sa triplă. Prin urmare, direcțiile conjugate pot fi utile pentru optimizarea sa. Cu toate acestea, mai mult decât
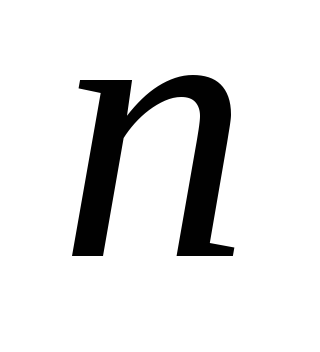
Aprobarea. Să i se dea o funcție patratică
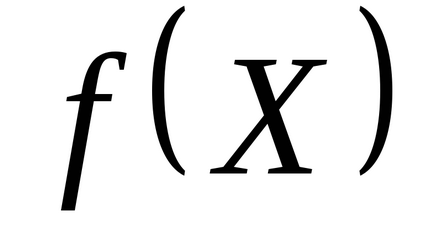
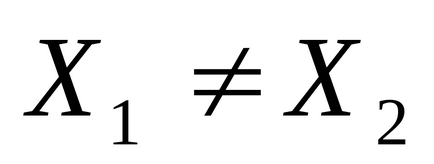
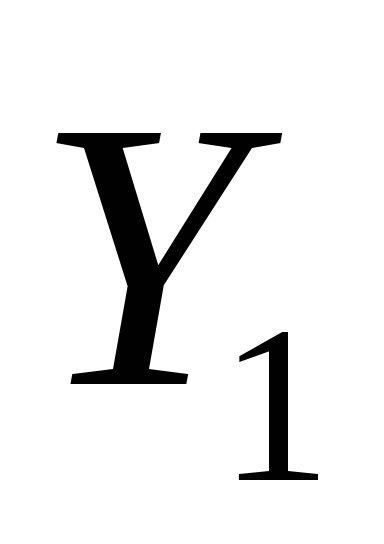
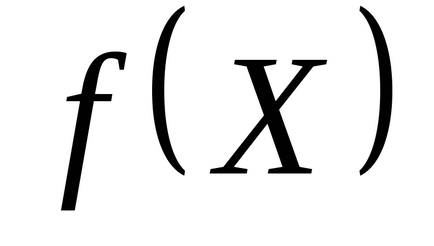
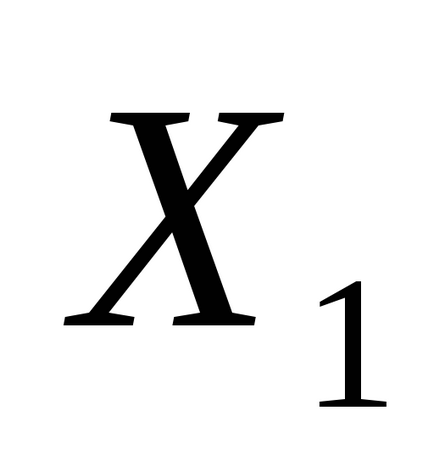
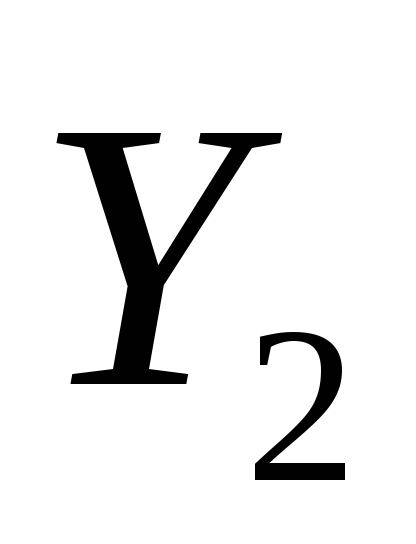
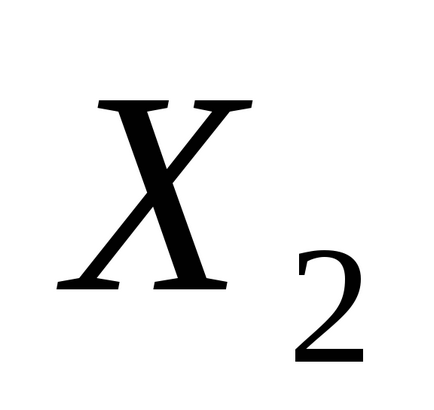
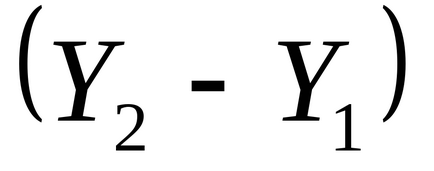
Pasul 1. Setați punctul de pornire
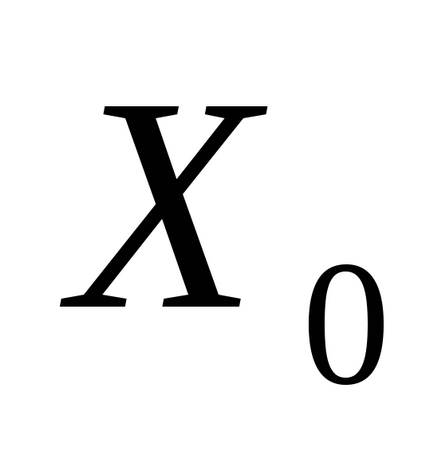
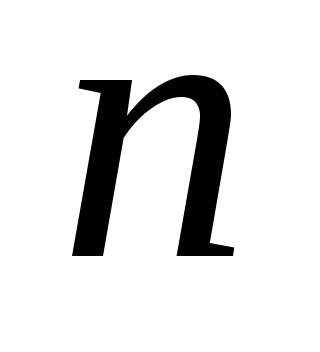

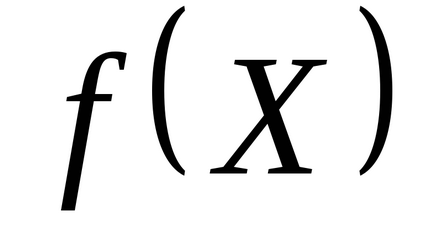
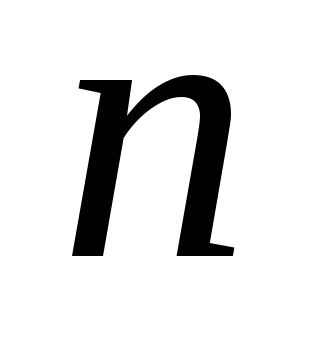
Pasul 2. Efectuați o etapă suplimentară
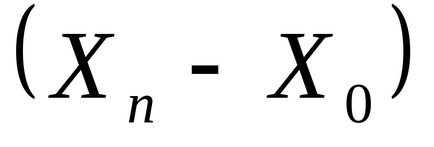
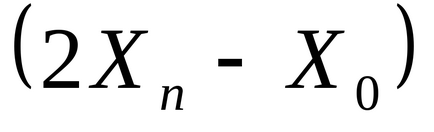
Pasul 3. Lăsați


și
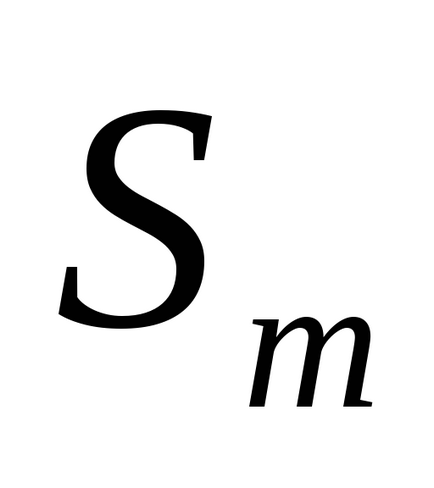

În cazul în care condițiile
(*)
atunci căutarea continuă de-a lungul direcțiilor originale

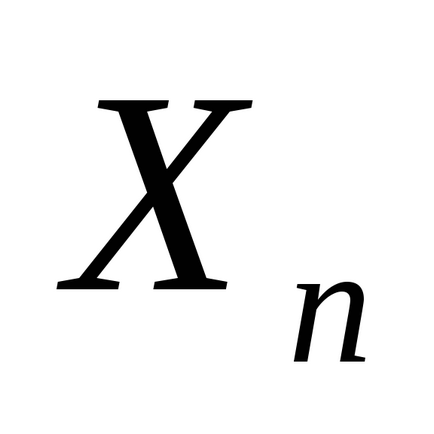
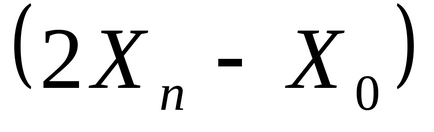
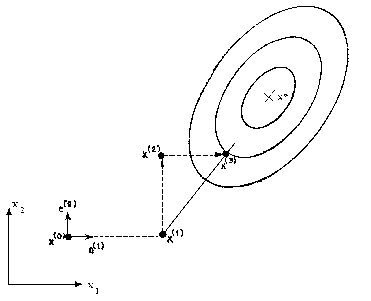
Pasul 4. Dacă condițiile

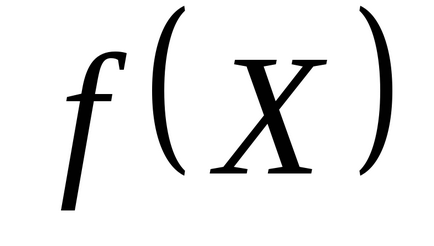
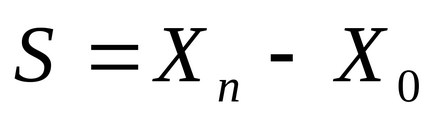
,
și anume direcție
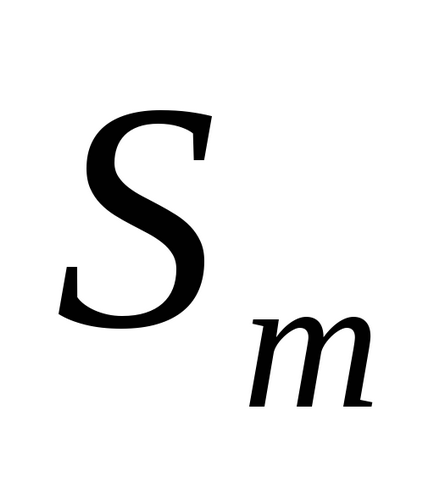

Pasul 5. Dacă
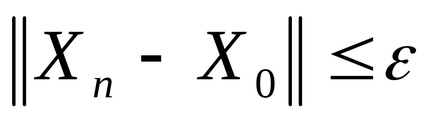
Un exemplu. Apăsând pe pictogramă se va deschide documentul Mathcad al metodei direcției conjugate, în care puteți efectua calcule.
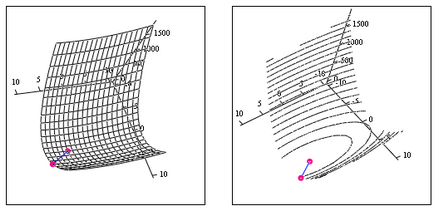
prin metoda direcției conjugate
Poate părea irațional să respingă direcția cea mai de succes iterației curente și de a stabili o nouă tendință promițătoare în ultimul loc în loc de prima. Cu toate acestea, este ușor de văzut că tendința cea mai de succes probabil în sine epuizat, și o nouă direcție promițătoare tocmai a fost folosit pentru optimizarea unidimensional și se aplică imediat, nu există nici un sens, deoarece promovarea pur și simplu să fie.
Powell a demonstrat că determinantul matricei direcției are o valoare maximă dacă și numai în cazul în care direcțiile

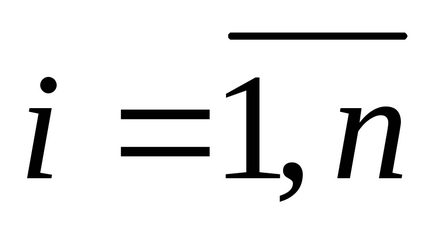
Se demonstrează că procedura Powell converge la un punct la care gradientul este zero dacă funcția obiectivă este strict convexă. Acest punct este un minim local. Metoda este foarte sensibilă la metoda de construire a direcțiilor conjugate și, prin urmare, depinde de precizia căutării unidimensionale utilizată. Powell a propus utilizarea unei secvențe de interpolări patrate cu o procedură specială pentru reglarea parametrilor acestei căutări liniare. Cu toate acestea, studiile numerice au arătat că metoda de direcții Powell conjugate nu ar trebui să fie utilizată pentru o dimensiune mai mare de 20.