Lucrare de laborator nr. 2.
Subiect: Studiul dependenței perioadei de oscilație a unui pendul de fir pe lungimea unui șir.
Echipament: un trepied cu un bar și un fir de cutie cu o buclă de la sfârșitul anului, cârlig de marfă, linie, cronometru electronic
Scopul lucrării este de a testa experimental formula referitoare la perioada oscilațiilor unui pendul cu lungimea suspensiei sale.
Luați în considerare oscilațiile unui pendul al firului, adică Un corp mic (de exemplu, o minge) suspendat pe un șir, lungimea căreia depășește considerabil dimensiunile corpului însuși. Dacă mingea este deviată din poziția de echilibru și eliberată, aceasta va începe să oscileze. La început, pendulul se mișcă cu o viteză crescătoare în jos. În poziția de echilibru, viteza mingii nu este egală cu zero și se mișcă în sus prin inerție. Când se atinge cea mai înaltă poziție, mingea începe să se miște din nou în jos. Vor fi oscilații libere ale pendulului.
Oscilațiile libere sunt oscilații care apar într-un sistem sub acțiunea forțelor interne, după ce sistemul a fost eliminat din poziția de echilibru stabil.
Mișcarea oscilantă este caracterizată de amplitudinea, perioada și frecvența oscilațiilor.
Amplitudinea oscilațiilor este cea mai mare deplasare a corpului oscilant din poziția de echilibru. Denumită de A. Unitatea de măsură - metru [1m].
Perioada de oscilație este timpul în care corpul efectuează o singură oscilație completă. Unitatea de măsură este cea de-a doua [1s].
Frecvența oscilațiilor este numărul de vibrații pe unitate de timp. Denunțat de ν. Unitatea de măsură este hertz [1Hz].
Organismul suspendat pe un fir inextensibil fără greutate se numește pendul matematic.
Perioada de oscilație a unui pendul matematic este determinată de formula: (1), unde l este lungimea suspensiei și g este accelerația datorată gravitației.
Perioada de oscilație a unui pendul matematic depinde de:
1) din lungimea firului. Perioada de oscilație a unui pendul matematic este proporțională cu rădăcina pătrată a lungimii filamentului. Ie de exemplu, atunci când lungimea firului este redusă cu un factor de 4, perioada scade cu un factor de 2; Când lungimea firului este redusă cu un factor de 9, perioada scade cu un factor de 3.
2) de accelerarea caderii libere a terenului în care au loc oscilațiile. Perioada de oscilație a pendulului matematic este invers proporțională cu rădăcina pătrată a accelerației datorată gravitației.
Corpul suspendat pe un arc este numit un pendul de primăvară.
Perioada de oscilare a pendulului de primăvară este determinată de formula, unde m este masa corpului, k este rigiditatea arcului.
Perioada de oscilație a pendulului de primăvară depinde de:
1) privind greutatea corporală. Perioada de oscilație a pendulului de primăvară este proporțională cu rădăcina pătrată a masei corpului.
2) din rigiditatea arcului. Perioada de oscilație a pendulului de primăvară este invers proporțională cu rădăcina pătrată a rigidității arcului.
În această lucrare, investigăm oscilațiile unui pendul matematic. Din formula rezultă că perioada de oscilație se schimbă de două ori atunci când lungimea suspensiei se modifică cu un factor de patru.
Aceasta este o consecință și este verificată în lucrare. Alternativ, se testează două penduluri, lungimea suspensiilor cărora se deosebesc de patru ori. Fiecare dintre penduluri este pusă în mișcare și se măsoară timpul pentru care se produce un anumit număr de oscilații. Pentru a reduce influența efectelor secundare, experimentul cu fiecare pendul este efectuat de mai multe ori și pentru a găsi timpul mediu petrecut de pendul pentru a efectua un anumit număr de oscilații. Apoi calculați perioadele pendulului și găsiți raportul.
1. Pregătiți un tabel pentru înregistrarea rezultatelor măsurătorilor și calculelor:
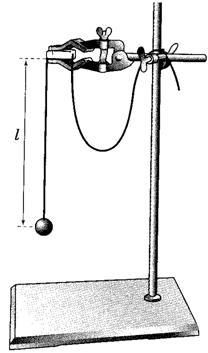
2. Fixați bara transversală în cuplajul din partea superioară a tijei trepiedului. Așezați trepiedul pe masă astfel încât capătul laturii să iasă dincolo de marginea suprafeței mesei. Așezați o încărcătură din set folosind un filet pe bara transversală. Distanța de la punctul de greblă până la centrul încărcăturii trebuie să fie de 25-30 cm.
3. Pregătiți cronometrul electronic pentru o funcționare manuală.
4. Înclinați sarcina la 5- 6 cm față de poziția de echilibru și se măsoară timpul în care sarcina 30 face oscilații complet (la sarcini ulterioare deviere a unghiului de deviere nu este mare).
5. Repetați măsurarea de 3-4 ori și determinați timpul mediu tσr1 = (t1 + t2 + t3 + t4) / 4
6. Calculați perioada de vibrație a încărcăturii cu o lungime de suspensie de 25-30 cm conform formulei.
7. Creșteți durata suspendării de patru ori.
8. Repetați seria de experimente cu un pendul cu o lungime nouă și calculați perioada de oscilații conform formulei.
9. Calculați frecvențele oscilațiilor pentru ambele penduluri prin formulele și.
10. Comparați perioadele de oscilații ale celor două penduluri, lungimea cărora se deosebește de patru ori și trageți o concluzie cu privire la valabilitatea formulei (1). Indicați posibilele motive pentru discrepanța dintre rezultate.
11. Răspunde la întrebările testului.
1. Ce se numește perioada oscilațiilor pendulului?
2. Ce se numește frecvența de oscilație a unui pendul? Care este unitatea de frecvență a vibrațiilor?
3. Din ce cantități și cum depinde perioada de oscilație a unui pendul matematic?
4. Din ce cantități și cum depinde perioada de oscilație a pendulului de primăvară?
5. Ce fluctuații se numesc proprii?