Teorema 2. Avionul care nu trece prin varful unui con circular drept, se trece într-o elipsă, în cazul în care intersectează toate generatoarele conului (vezi. Ris.190), o parabolă în cazul în care este paralelă cu doar unul dintre conului (vezi. Ris.191) și hiperbolă dacă este paralelă cu două generatoare ale conului (vezi. ris.192).
Dovada. Pentru dovadă, să luăm în considerare un con circular drept, care în sistemul de coordonate dreptunghiular este descris de ecuația:
și obținută geometric prin rotirea în jurul axei liniei drepte. aparținând planului de coordonate. Prin simetrie suprafață circulară (6) poate fi limitată doar la secțiunile de la avioane Pomeau-supă perpendicular coordonate-ASW-plane. Ecuațiile corespund unor astfel de planuri. .
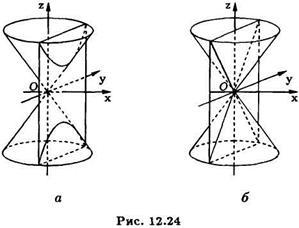
În cazul în care. atunci planul secant este descris de ecuatie. unde și este paralelă cu planul de coordonate. Substituind valoarea abscisei conului în ecuația (6), descoperim că secțiunea transversală în planul descris de ecuația și definește o hiperbolă echilateral (A se vedea. Ris.12.24), în timp ce o pereche de linii care sunt generatoare ale conului. Ris.12.24.
Acum permiteți coeficientul din ecuația planului de tăiere. Apoi avionul poate fi reprezentat de o ecuație. în cazul în care. . În virtutea simetriei conului față de plan, este suficient să ne limităm la cazul când.
Secțiunea conică pentru planul examinat în spațiu va fi descrisă printr-un sistem de două ecuații (7)
Pentru a obține ecuația planului secant, ia în considerare un sistem de coordonate dreptunghiular,
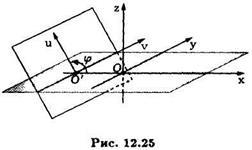
și luând ca axe de coordonate liniile care sunt intersecția planului secant cu planurile de coordonate u (vezi figura 12.25).
Coordonatele și un punct arbitrar în planul de tăiere vor fi asociate coordonatelor sale. și în spațiu de relațiile:
unde este unghiul dintre secțiunea conică perpendiculară pe planul de coordonate. și planul coordonatelor. și. a.
Înlocuind (8) în prima ecuație a sistemului (7), adică în ecuație. obținem ecuația secțiunii conice din sistemul de coordonate:
. Extinzând parantezele și oferind astfel de termeni, găsim:
Când. când planul de tăiere formează un plan cu același unghi ca formând secțiunea conică va fi o parabole conului (vezi fig ..) și este descris de ecuația:
Prin modificarea parametrului în ecuația planului de tăiere, orice parabolă poate fi obținută ca o secțiune conică.
Când. Ecuația (9) are forma:
Aici există două opțiuni. Când. și anume când avionul secantă formează cu un unghi mai mic decât formarea inegalității și, conul prin urmare, ecuația (10) este o ecuație secțiune conică a elipsei (A se vedea. Fig. 12.26) vor fi îndeplinite.
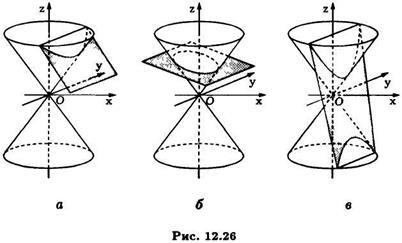
Și aici, variind parametrii în ecuația planului de tăiere, putem obține o elipse în secțiune.
Când. și anume Atunci când planul secant se formează un unghi mai mare cu planul decât generatoarele conului, avem. astfel încât secțiunea conică descrisă de ecuația (10) va fi o hiperbolă (vezi Fig.). Variind parametrii și se poate obține orice hiperbolă în secțiunea conică.