Calcularea puterii mecanismului inițial. Determinarea forței de contrabalansare și a momentului de contrabalansare. Teorema N.E. Zhukovsky pe pârghia tare.
Calcularea puterii mecanismului inițial
Mecanismul inițial constă într-o legătură de vârf care intră în perechea cinematică rotativă sau translată cu suportul.
Lanțul cinematic va fi determinat static în condiții. Mecanismul inițial pentru n = 1 și p1 = 1 nu va fi în echilibru. Pentru ca mecanismul inițial să fie în echilibru, este de asemenea necesar să se introducă o forță de contrabalansare sau un moment de contrabalansare. care ar echilibra toate forțele și momentele atașate la legătura de conducere.
Balanțele forță contrabalans momentyavlyayutsya asemenea forță sau un cuplu care trebuie aplicată elementului de conducere pentru mecanismul să se deplaseze printr-o anumită lege sau ținut într-o poziție predeterminată.
Ceea ce acționează asupra legăturii de deplasare sau depinde de modul în care energia este transferată de la motorul electric la arborele cotit. Următoarele cazuri sunt posibile.
1. Arborele cotit al motorului este conectat la arborele mașinii de lucru printr-un ambreiaj (figura 6.1). În acest caz, se aplică un cuplu de echilibrare arborelui.
Greutatea legăturii: m1 = 2 kg. Accelerarea centrului de masă al legăturii. = 2,95 m / s 2.
1) Determinarea gravității legăturii:
2) Determinarea forței de inerție:
Forța de inerție este îndreptată în direcția opusă accelerației.
Să construim mecanismul inițial pe o scară de 1: 5.
Arătăm toate forțele care acționează asupra ei, reacția necunoscută R61 și momentul de contrabalansare
1. Să găsim valoarea momentului contrabalansării.
Se scrie ecuația momentelor tuturor forțelor în raport cu punctul O1.
Planul de forță pentru mecanismul inițial
Momentul de echilibrare este:
Aici. Lungimile brațelor h1 și h2 sunt măsurate în schema de proiectare și înmulțite cu scara.
Să compunem ecuația vectorială a echilibrului tuturor forțelor care acționează asupra mecanismului inițial.
Alegem scara planului de forță mF = 0,5.
Se calculează valorile segmentelor corespunzătoare vectorilor de forță. Datele vor fi enumerate în Tabelul 1:
Construim un plan de forțe. În concordanță cu ecuația vectorială, complotăm segmentele corespunzătoare vectorilor. . . Vectorii pot fi amânați în orice ordine. Legând începutul primului vector și sfârșitul ultimei, obținem un poligon al forțelor și un segment care definește reacția. Măsurarea lungimii sale și înmulțirea cu scala mF. obținem valoarea reacției. Datele sunt prezentate în Tabelul 1.
2. Arborele motorului este conectat la arborele mașinii de lucru cu ajutorul unei transmisii de angrenaj (figura 6.2). În acest caz, forța de contrabalansare este aplicată arborelui motorului, care acționează de-a lungul liniei de cuplare.
Greutatea legăturii: m1 = 2 kg. Accelerarea centrului de masă al legăturii. = 2,95 m / s 2.
1) Determinarea gravității legăturii:
2) Determinarea forței de inerție:
Forța de inerție este îndreptată în direcția opusă accelerației.
Să construim mecanismul inițial pe o scară de 1: 5.
Arătăm toate forțele care acționează asupra ei, reacția necunoscută R61 și forța de echilibrare Fur. care se aplică perpendicular pe pârghia AO1 la punctul A.
Planul de forță pentru mecanismul inițial
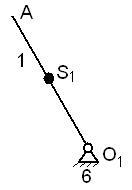
1. Găsiți amploarea forței de echilibrare Fur.
Se scrie ecuația momentelor tuturor forțelor în raport cu punctul O1.
Forța de egalizare Fur este egală cu:
Aici. Lungimile brațelor h1 și h2 sunt măsurate în schema de proiectare și înmulțite cu scara.
Să compunem ecuația vectorială a echilibrului tuturor forțelor care acționează asupra mecanismului inițial.
Alegem scara planului de forță mF = 0,5.
Se calculează valorile segmentelor corespunzătoare vectorilor de forță. Datele vor fi enumerate în Tabelul 2:
Construim un plan de forțe. În concordanță cu ecuația vectorială, complotăm segmentele corespunzătoare vectorilor. . . . Vectorii pot fi amânați în orice ordine. Legând începutul primului vector și sfârșitul ultimei, obținem un poligon al forțelor și un segment care definește reacția. Măsurarea lungimii sale și înmulțirea cu scala mF. obținem valoarea reacției. Datele sunt prezentate în Tabelul 2.
Teorema privind controalele rigide N.E. Zhukovsky
Zhukovsky a arătat că mecanismul de echilibru cu un grad de libertate corespunde unui braț echilibru, și a propus o metodă de construcție și de încărcare a pârghiei. Teorema lui NE Zhukovsky poate fi formulată după cum urmează:
Dacă vectorii tuturor forțelor aplicate la diferite puncte de pe link-urile și mecanismul de echilibru pentru a trece paralel cu ele însele, în același punct numele Rotită 90 ° viteze planificați luând forma unui plan pentru o pârghie tare, suma momentelor acestor forțe cu privire la planul de pol va fi zero.
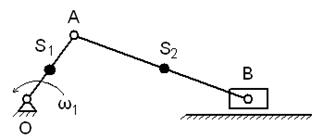
Pentru mecanismul glisorului, determinați forța de echilibrare.
1. Aplicăm o forță de egalizare la punctul A perpendicular pe AO. Să construim
planificați vitezele și rotiți-o cu 90 °. Punctele corespunzătoare viteze Planul va face vectorii forță, menținând în același timp direcția lor, momentul în care am înlocui perechea de forțe, iar fiecare forță va muta planul.
2. Să calculam ecuația momentelor tuturor forțelor cu privire la pol:
Rezolvând ecuația, obținem:
Lungimea tuturor umerilor este măsurată în schema de calcul.
Planul de viteză a fost rotit cu 90 ○
Astfel, cu ajutorul teoremei lui Zhukovskii, putem:
1. Determinați forța de echilibrare. nu efectuarea calculului puterii;
2. Verificați valoarea forței de contrabalansare. obținută din calcularea puterii. Eroarea calculelor este%. Eroarea nu trebuie să depășească 20%.