Se dovedește că $ MN || AD \ și \ MN = \ frac $.
Luați în considerare vectorul $ \ overrightarrow $. Acum folosim regula poligonului pentru a adăuga vectori. Pe de o parte, descoperim asta
Pe de altă parte
Adăugăm ultimele două egalități pe care le obținem
Din moment ce $ M $ și $ N $ sunt punctele medii ale laturilor trapezului, avem
Din aceeași egalitate (din moment ce $ \ overrightarrow $ și $ \ overrightarrow $ sunt co-directionale și, prin urmare, collinear), obținem acel $ MN || AD $.
Exemple de probleme privind noțiunea liniei mediane a unui trapez
Partea laterală a trapezoidului este egală cu $ 15 \ cm $ și respectiv $ 17 \ cm $. Perimetrul trapezoidului este egal cu $ 52 \ cm $. Găsiți lungimea liniei de mijloc a trapezului.
Indicăm linia de mijloc a trapezoidului în termeni de $ n $.
Suma laturilor este
\ [15 \ cm + 17 \ cm = 32 \ cm \]
În consecință, deoarece perimetrul este egal cu $ 52 \ cm $, suma bazelor este
\ [52 \ cm-32 \ cm = 20 \ cm \]
Prin urmare, prin teorema 1, obținem
Capetele diametrului cercului sunt separate de tangenta lui de $ 9 $ cm si respectiv $ 5 $ cm. Gasiti diametrul acestui cerc.
Să dăm un cerc cu centrul la punctul $ O $ și diametrul $ AB $. Desenați tangenta $ l $ și construiți distanțele $ AD = 9 \ cm $ și $ BC = 5 \ cm $. Tragem raza $ OH $ (figura 2).
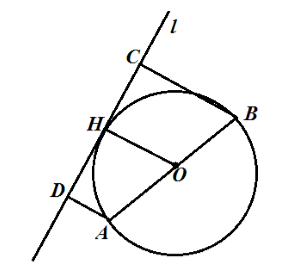
Deoarece $ AD $ și $ BC $ sunt distanțe față de tangenta, $ AD \ bot l $ și $ BC \ bot l $ și din moment ce $ OH $ este o rază, atunci $ OH \ bot l $, deci $ OH | \ left | AD \ right || BC $. Din aceasta, vedem că $ ABCD $ este un trapez, iar $ OH $ este linia de mijloc. Prin teorema 1, obținem
\ [d = 2OH = 2 \ cdot 7 \ cm = 14 \ vezi \]