Printre modelele compoziționale, se evidențiază un grup special de mijloace, numit "serii ritmice și metrice".
Ritmul este alternanța obișnuită a elementelor în timp și spațiu. Ritmul este cel mai universal mod de a construi o formă artistică. Este folosit nu numai în compoziția arhitecturală, ci în toate celelalte forme de artă. Deoarece arhitectura este o artă spațială, modelele repetării trebuie să se refere nu numai la volumele și elementele structurii, ci și la intervalele spațiale dintre ele. În DIC, se distinge un ritm natural și liber. În ultimul caz, caracteristicile schimbării elementelor nu sunt de natură "matematică" rigidă.
O variantă specială a ritmului, folosind doar modelul repetiției stricte, se numește "metru". Gama Metric joacă un rol important în situațiile spațiale reale: crearea unui fel de „conducător“, cu lungimi egale, permite estimarea vizuală mai precisă a distanței, se elimină un efect de perspectivă și facilitează orientarea în spațiu. Principiile organizării metrice și ritmice (inclusiv exemple de ritm liber) sunt prezentate în Fig. I.8. Rețineți că efectul de perspectivă creează vizual o impresie ritmică a seriei metrice (Figura I.8, a-d). În Fig. I.8-b reprezintă seria metrică de elemente spațiale vizibile (deschideri arcuite) în combinație cu un număr de suporturi masive. Fig. 8-in oferă o idee despre utilizarea seriei metrice și ritmice în soluția fațadei clădirii. Pliurile din Fig. I.8-d este un exemplu al unui ritm liber natural.

Fig. I.8. Seriile ritmice și metrice:
a) Partenonul, Atena; b) Apeductul, Segovia; c) un fragment din fațada Catedralei Notre-Dame din Paris; d) seria metrică din interiorul templului lui Amun, Karnak; e) falduri pe tesatura - un exemplu de ritm liber.
Proporționarea este una dintre cele mai importante metode de construire a unei forme arhitecturale armonioase. Word proporție (. Lat Proportio) înseamnă o co-dimensiuni părți de relații-shenie împreună (grecii antici foloseau cuvântul analogie - similitudine, implicând similitudine a pieselor care constituie unitatea, unul de altul și de la întreg). Conceptul de proporție este folosit în trei semnificații de bază.
Primul înseamnă raportul parametrilor de bază ai formei (lungime, lățime, înălțime). Acesta este sensul care se înțelege atunci când se vorbește despre proporțiile unui anumit lucru, inclusiv clădire. Proporția aici caracterizează obiectul ca un întreg, formează baza imaginii sale, statică (de exemplu, un cub) sau dinamică (prisma alungită).
Al doilea înțeles este egalitatea rapoartelor măsurii cantitative, în formă matematică este scrisă ca a / b = c / d. Acest înțeles al conceptului de "proporție" este folosit în marea majoritate a lucrărilor dedicate problemei proporțiilor din arhitectură. Exemplul cel mai obișnuit în arhitectură este formarea de forme bazate pe dreptunghiuri similare, ale căror diagonale sunt fie paralele (proporție directă) sau perpendiculare (proporția inversă) (a se vedea figura I.9).
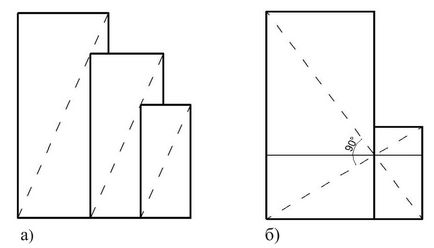
Fig. I.9. Crearea relațiilor directe a) și inverse b) relațiile proporționale folosind diagonalele paralele și perpendiculare ale dreptunghiurilor.
În al treilea. mai general, sub proporția din arhitectură se înțelege orice regularitate în raportul cantităților, care conectează părțile individuale și parametrii formei într-un singur întreg.
Tipuri de relații proporționale. În teoria și practica arhitecturii, progresele armonice armonice și geometrice sunt cele mai cunoscute.
O progresie aritmetică este exprimată printr-o serie de numere, în cazul în care fiecare număr ulterior mai mare decât cel precedent și aceeași valoare (cel mai simplu exemplu - un număr natural de la 0, 1, 2, 3, 4, 5, etc.), a cărui imagine poate fi un interval de măsurare obișnuit . O progresie armonică este o serie de numere care sunt inversate la o serie de numere de progresie aritmetică, de exemplu: 1/2, 1/3, 1/4, 1/5, 1/6, 1/7. De asemenea, el se află în centrul sistemului muzical.
O progresie geometrică este o serie de numere în care fiecare număr succesiv este mai mare (sau mai mic) decât cel precedent cu același număr de ori. De exemplu: 1, 2, 4, 8, 16. 1, 1/2, 1/4, 1/8, l / 16. Raportul dintre termenii vecini ai seriei geometrice pe toată lungimea sa rămâne constant.
Serii de aditivi se bazează pe sumarea numerelor. Serii deosebit de importante Fibonacci (1, 2, 3, 5, 8, 13, 21, 34), Fiecare membru ulterior, începând cu al treilea, este egal cu suma celor precedente. Raportul dintre termenii adiacenți din această serie tinde, în limită, la valoarea "secțiunii de aur" (1.618 ...). Termenul „secțiunea de aur“ a fost introdus Leonardo da Vinci pentru a forma un alt pitagoreici divid segmentul în așa-numitul „extremă și raportul mediu“, în care cea mai mare parte este proporțională între segmentul de mijloc și toată porțiunea inferioară. Dacă lungimea unui segment este luată ca una, atunci părțile sale vor fi exprimate prin numere iraționale x = 0.618 ..., a - x = 0.382. Pe baza acestor numere se poate obține o serie geometrică. - 0,146 - 0,236 - 0,382 - 0,618 - 1 - 1,618 - 2,618 - 4,236 - 6,854 -. Descoperit prin examinarea unei game largi de fenomene de natură, artă și arhitectură. Secțiunea de aur se numește „proporția divină“ și ia în considerare legile universale ale sale Express, de obicei, 1.618 sau numărul său invers 0618, care a adoptat simbolurile F și 1 / F. Metoda geometrică de divizare a segmentului într-o "secțiune de aur" este prezentată în Fig. I.10. Se compune din următoarele. În două pătrate adiacente se trasează diagonala (AE). Apoi, un arc este extras din volumul E cu o rază egală cu CE la intersecția cu diagonala (adică D). După aceasta, din arcul A, raza AD este trasă la intersecția cu orizontala (adică B). Rezultatul B divizează segmentul AC în raport cu secțiunea de aur, adică AB / BC = F.
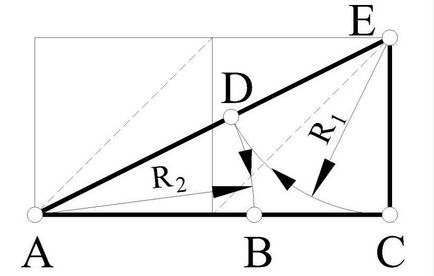
Fig. I.10. Metoda geometrică de construire a unei "secțiuni de aur".