O bijecție este o cartografiere. care este simultan surjectiv. și injectiv. Într-o cartografie bijectivă, fiecare element al unui set corespunde exact unui element al celuilalt set și este definită o cartografie inversă care are aceeași proprietate. Prin urmare, o cartografiere bijectivă este numită și o cartografiere unu-la-unu (corespondență), o cartografiere unu-la-unu.
Dacă se poate stabili o corespondență unu-la-unu (bijecție) între două seturi, atunci se consideră că astfel de mulțimi sunt echivalente. Din punctul de vedere al teoriei seturilor. seturile echipotent sunt indistinguizabile.
O cartografiere unu-la-unu a unui set finit în sine se numește permutare (sau substituire) a elementelor din acest set.
Definiție [ ]
Exemple [ ]
Proprietăți [ ]
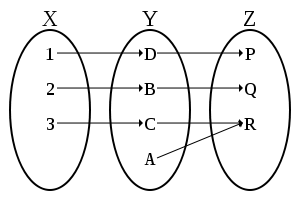
- Funcția f. X # x2192; Y este bijectiv dacă și numai dacă există o funcție inversă f # x2212; 1. Y # x2192; X: Y \ to X> astfel încât
- Dacă funcțiile f și g sunt bijective, atunci compoziția g # x2218; f este bijectiv, în acest caz (g # x2218; f) # x2212; 1 = f # x2212; 1 # x2218; g # x2212; 1 = circulație. Pe scurt: compoziția bijecțiilor este o bijecție. Totuși, inversul nu este adevărat: dacă g # x2218; f este bijectiv, atunci putem spune doar că f este injectiv și g este surjectiv.