Această egalitate deține (și seria converge) pentru orice real x. și pe întregul plan complex. conform lui D'Alembert. Secvența numitorilor formează secvența A007680 în OEIS.
- Funcția de eroare la infinit este unitatea; Totuși, acest lucru este valabil numai când se apropie infinitul de-a lungul axei reale, deoarece:
- În considerarea funcției de eroare în planul complex, punctul z = ∞ este în esență unic pentru el.
- Derivatul funcției de eroare este derivat direct din definiția funcției:
- Funcția de eroare inversă este o serie de
Prin urmare, seriile pot fi reprezentate în următoarea formă (rețineți că fracțiunile sunt reduse):
Secvențele numărătorilor și numitorilor după abreviere - A092676 și A132467 în OEIS; succesiunea numărătorilor înainte de abrevierea este A002067 în OEIS.
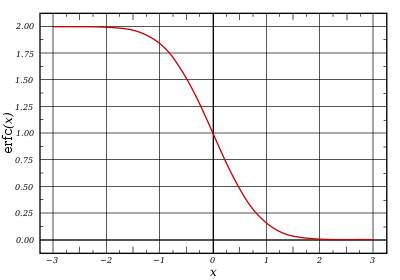
Funcție suplimentară de eroare
Funcția de eroare și o funcție de eroare suplimentară sunt întâlnite în rezolvarea anumitor ecuații diferențiale, de exemplu, ecuația de căldură cu condițiile limită descrise de funcția Heaviside ("pas").
În sistemele de comunicații optice digitale, probabilitatea de eroare pe bit este de asemenea exprimată printr-o formulă care utilizează funcția de eroare.
Pentru x mare, este utilă o extensie asimptotică pentru funcția de eroare suplimentară:
Deși această serie diferă pentru orice x finit, în practică primii câțiva termeni sunt suficienți pentru a calcula erfc x \, x> cu o precizie bună, în timp ce seria Taylor converge foarte lent.
O altă aproximare este dată de formula
Funcția inversă la Φ. cunoscută ca o funcție cuantică normală, este uneori denumită probit> și este exprimată în termenii funcției de eroare normală caDistribuția integrală integrală este mai des utilizată în teoria probabilităților și în statisticile matematice, în timp ce funcția de eroare este mai des utilizată în alte secțiuni ale matematicii.
Funcția de eroare este un caz special al funcției Mittag-Leffler. și poate fi reprezentată și ca o funcție hipergeometrică degenerată (funcția Kummer):
Funcția de eroare este, de asemenea, exprimată în termeni de integrate Fresnel. În ceea ce privește funcția gamma incompletă regularizată P și o funcție gama incompletă,
Funcții de eroare generalizate
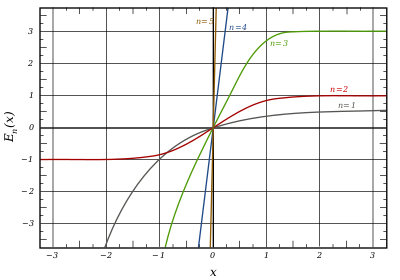
Cazurile notabile sunt:
După împărțirea cu n. toate E n> cu n ciudat arata ca (dar nu identice). Tot E n> cu even n arata, de asemenea, similare, dar nu identice, dupa divizarea cu n. . Toate funcțiile de eroare generalizate cu n> 0 arată asemănătoare cu semi-axa x> 0.
La jumătatea liniei x> 0, toate funcțiile generalizate pot fi exprimate în funcție de funcția gamma:
În consecință, putem exprima funcția de eroare prin intermediul funcției gamma:
Integrări iterate ale funcției de eroare adițională
Integalele iterative ale funcției de eroare suplimentare sunt definite ca
i n erfc z = ∫ z ∞ i n - 1 erfc ζ d. \, \ numele operatorului \, z = \ int \ limitele _ ^ i ^ \, \ operatorname \, \ zeta \, d \ zeta.
Ele pot fi extinse într-o serie:
din care urmează proprietățile de simetrie
În limba Java, biblioteca standard de funcții matematice java.lang.Math nu conține [1] o funcție de eroare. Clasa Erf poate fi găsită în pachetul org.apache.commons.math.special din biblioteca non-standard furnizată de [2] Apache Software Foundation.
În Python, funcția de eroare este disponibilă [3] din biblioteca matematică standard. începând cu versiunea 2.7. De asemenea, funcția de eroare, o funcție de eroare suplimentară și multe alte funcții speciale sunt definite în modulul special al proiectului SciPy [6].
În limba Erlang, funcția de eroare și o funcție suplimentară de eroare sunt disponibile din modulul matematic standard [4].