atunci T (N) = N ln N. pentru toate N = 2 k. k> 1.
2. Când căutăm un element dat utilizând metoda de căutare liniară (exercițiul 2 al algoritmului de inserție), se face o comparație cu elementele de la începutul matricei. În matricea sortată, puteți utiliza compararea elementului căutat cu mijlocul matricei, apoi selectați partea în care acesta va fi localizat și pentru această parte repetați separarea recursivă și așa mai departe -
a căutat. Scrieți un program care implementează acest algoritm și dovedește că timpul său este Θ (ln N).
3. Bucla în timp în procedura Insertion_Sort se uită prin toate elementele secțiunii sortate într-un rând. În schimb, puteți utiliza metoda binară
(exercițiul 2 al algoritmului de sortare a fuziunii) pentru a găsi punctul de inserție în timp Θ (ln N). Scrieți implementarea corespunzătoare a procedurii
Insertion_Sort și determinați dacă va fi posibil în acest fel ca timpul total de funcționare să fie egal cu Θ (N ln N).
Mergeți algoritmul de sortare
4. Fie ca tipurile de inserare și îmbinare să fie executate pe aceeași mașină și necesită operațiuni 8 N 2 și 64 N nn N, respectiv. Pentru care valori ale lui N este mai eficientă sortarea inserției? Cum pot îmbunătăți algoritmul de sortare a fuziunii?
5. La o valoare minimă a lui N, un algoritm care necesită operațiuni 100 N 2 este mai eficient decât un algoritm care necesită operațiuni de 2 N.
1. Sortarea asimptotică a unei îmbinări este mai rapidă decât sortarea prin inserturi, dar pentru valori mici de N raportul este invers. Prin urmare, este logic ca piesele scurte să nu se mai separe și să se sorteze prin inserturi.
1.1. Fie matricea mărimei N împărțită în k părți ale mărimii N k. Arată asta
Puteți sorta toate piesele în mod individual (folosind sortarea inserției) în timp Θ (kN).
1.2. Arătați că după sortare, puteți îmbina toate piesele într-o singură matrice ordonată într-un timp Θ (N ln (N k)).
1.3. Timpul mediu de rulare al unui astfel de algoritm mixt este Θ (Nk + N ln (N k)). Care este rata maximă de creștere k în funcție de
N. la care acest timp este încă egal cu Θ (NInN)?
1.4. Cum se determină valoarea optimă a k în practică.
2. Fie matricea un [1. N] dat. O inversiune în această matrice este o pereche de numere i
2.1. Care este numărul maxim de inversiuni dintr-o matrice de lungime N.
2.2. Cum este legat timpul de lucru al algoritmului de inserție și numărul de inversiuni? Explicați-vă răspunsul.
2.3. Construiește un algoritm care numără numărul de inversiuni într-o matrice de lungime N în timp Θ (N ln N).
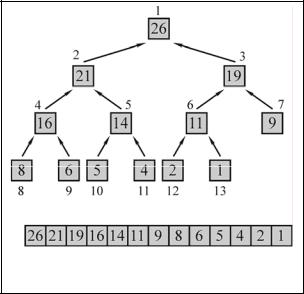
Figura 3 - Exemplu de heap binar
Algoritmul de sortare cu heap (Heap)
Algoritmul de sortare cu heap (Heap)
Sortarea cu un heap necesită timpul T (N) = Θ (N ln N) pentru munca sa. Dar spre deosebire de algoritmi de îmbinare nu este nevoie de o astfel de mare
cantitatea de memorie suplimentară pentru stocarea variabilelor. Adică, algoritmul combină avantajele algoritmilor de sortare a inserției (utilizarea unei cantități mici de memorie suplimentară) și metoda de fuzionare (timpul redus de lucru).
Structura de date utilizată de algoritm este numită heap binar, este convenabilă atunci când se utilizează cozile prioritare.
O grămadă binară este o matrice cu anumite proprietăți de ordonare. Pentru a formula proprietățile, vom trata matricea ca un arbore binar. Fiecare vârf al copacului corespunde unui element - figura 3.
Dacă vârful are indicele i. atunci părintele său are indicele int (i / 2). dar ea
2 i și 2 i + 1. Vârful cu indexul i = 1 este rădăcina. În memorie, matricea a este stocată. lungimea lui N și un parametru special Heap _ Size - dimensiunea heap și
Heap _ Mărime ≤ N. Mormântul constă din elementele a [1] ... a [Heap _ Size]. Trei funcții sunt utilizate pentru a vă deplasa în jurul mulțimii:
Elementele stocate în heap trebuie să aibă proprietatea de bază a heapului: pentru toate elementele, cu excepția rădăcină, condiția a Parent (i) ≥ a [i],
adică valoarea copilului nu trebuie să fie mai mare decât strămoșul, ceea ce înseamnă că rădăcina copacului este elementul maxim.
Înălțimea vârfului arborelui este înălțimea subtreei cu rădăcina la acest vârf (numărul de margini din calea cea mai lungă, începând din partea de sus în jos a copacului). Înălțimea copacului coincide cu înălțimea rădăcinii.
În arborele care formează grămada, toate nivelele, cu excepția celui din urmă, sunt complet umplute, astfel încât înălțimea acestui arbore este Θ (ln N). unde N este un număr
elemente în halbă.
Luați în considerare procedurile de bază pentru a lucra cu o grămadă:
1. Heapify - suporta proprietatea haldei de baza, timpul de executie este
Algoritmul de sortare cu heap (Heap)
2. Build_Heap - construiește un heap din matricea originală nesortată, timpul de execuție este Θ (N).
3. Heap_Sort - sortarea fără a folosi memorie suplimentară, timpul de execuție Θ (N ln N).
4. Extract_Max (eliminarea celui mai mare) și Insert (insert) sunt folosite pentru a crea o coadă cu priorități bazate pe heap. Timpul de funcționare al ambelor proceduri este Θ (ln N).
Menținerea proprietății nucleului Heap
Parametrii procedurii Heapify (a, i) sunt array a și index i. Se presupune că substrele cu rădăcinile Stânga (i) și Dreapta (i) au deja proprietatea principală. Procedura rearanjează elementele subdirecte cu vârful i. după care va avea proprietatea de bază. Ideea este simplă: dacă proprietatea principală nu este posibilă pentru un vârf, atunci ar trebui să fie schimbată cu un mare număr de descendenți ai acesteia și așa mai departe, până când elementul "se pliază" în locul dorit.
Luați în considerare procedura Heapify (A, i)
3 dacă (L≤Heap_Size) și (a [L]> a [i])
4 apoi cel mai mare: = L
5 altul Cel mai mare: = R
6 dacă (R≤Heap_Size) și (a [R]> a [Largest])
7 apoi cel mai mare: = R
9 apoi Schimb (a [i], un [Cel mai mare])
Variabila cea mai mare plasează indexul celui mai mare dintre elementele a [i],
o stânga (i) și o dreaptă (i). Dacă, la sfârșitul ciclului, cel mai mare = i. atunci elementul [i] este deja
"Immersat" în locul potrivit și procedura a fost terminată. În caz contrar, procedura schimbă un [i] și un [Cel mai mare]. dar este posibil să fi existat o încălcare
proprietatea principală din subarborele cu cel mai mare vârf, iar procedura Heapify este chemată în mod repetat pentru a elimina posibila încălcare.
Momentul de execuție cel mai rău pentru această procedură este T (N) = Θ (ln N).
Fie matricea o [1.N] dată. care ar trebui transformat într-o grămadă. Pentru a face acest lucru, puteți utiliza procedura Heapify. aplicând-o la rândul său la toate vârfurile, începând cu cele inferioare. Vârfurile cu numerele [N 2] + 1 ... N sunt frunze,
substraturile cu aceste frunze satisfac deja deja proprietatea de bază a heapului. Pentru fiecare dintre vârfurile rămase, în ordinea descrescătoare a indicilor,
2 Pentru i: = int (N / 2) downto 1 nu
Timpul maxim de funcționare al procedurii este T (N) = Θ (N).
Sortare cu o grămadă
Algoritmul de sortare constă din două părți, prima este procedura Build_Heap. transformând matricea într-o grămadă.
Cea de-a doua parte comandă direct mormanul. Elementul maxim al mormanului este în rădăcina copacului - elementul a [1]. Acest element variază de la un loc la altul
elementul [N]. dimensiunea memoriei scade cu 1 și restabilește proprietatea de bază a grămezii la vârful rădăcină (ca în subarborele înrădăcinate stânga (1) și la dreapta (1) proprietatea de bază a gramada nu este perturbat) prin procedura Heapify.
După aceea, maximul elementelor rămase va fi în rădăcină. Apoi se efectuează o permutare a [1] și o [N - 1]. Și din nou procedura este efectuată
Permutarea elementelor continuă până când se ordonează întreaga matrice.
2 Pentru i: = N downto 2 nu
Timpul de funcționare al procedurii este T (N) = Θ (N ln N).
În practică, algoritmii de sortare a heapului nu sunt cei mai rapizi, însă halda însăși ca o structură a acestor frecvențe este utilă.
Cozi cu priorități
O coadă cu priorități (coada de priorități) este un set ale cărui elemente vor fi considerate numere. În practică, elementele setului S sunt perechi
chom, α - informații legate de acesta; această informație este stocată lângă element și se mișcă cu ea, fără a afecta procesarea acesteia. Pentru simplitate, omitem descrierea lucrării cu date suplimentare.
Sunt posibile următoarele operații în coada de așteptare cu priorități:
1. Introduceți (S, x) adaugă un element x la setul S;
2. Maximum (S) returnează cel mai mare element al setului;
3. Extract_Max (S) elimină din set cel mai mare element;
4. Extract_Min (S) elimină din set cel mai mic element.
O coadă de priorități poate fi folosită, de exemplu, într-un sistem de operare de partajare a timpului. În același timp, stochează lista de sarcini cu prioritate
Algoritmul de sortare cu heap (Heap)
tetami. Imediat ce se termină următoarea sarcină, lucrarea cu prioritate maximă (operația Extract_Max) este selectată din coadă. Funcțiile noi se adaugă la coadă cu ajutorul funcției Inserare.
O altă aplicație a aceleiași structuri este simularea bazată pe evenimente. Coada conține evenimente și prioritatea este determinată de momentul în care ar trebui să apară evenimentul. Evenimentele trebuie modelate în ordinea în care apar. Selectarea următorului eveniment se face utilizând operația Extract_Min. adăugați evenimente - utilizând operația
Vom păstra elementele setului sub formă de heap. Elementul maxim este la rădăcină, astfel încât operația Maximum necesită timp Θ (1).
Pentru a elimina elementul maxim din coadă, trebuie să acționați în același mod ca atunci când sortați: