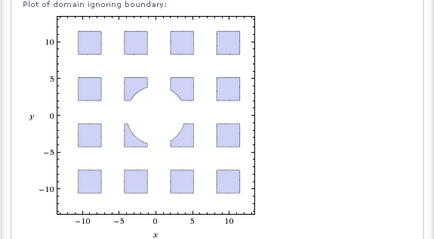
Cum să găsim domeniul unei funcții a două variabile?
În Wolfram | Alpha, pentru a găsi domeniul de aplicare al definiției funcției, utilizați interogarea domeniului. Aplicând această interogare la o funcție a două variabile, obținem următoarele:- domeniu sqrt (x ^ 2-y ^ 2x)
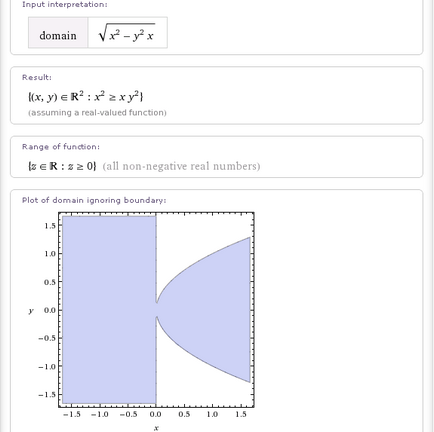
În general, această întrebare privind domeniul de aplicare al definiției unei funcții a două variabile în Wolfram | Alpha este epuizată. Apoi, am vrut doar să văd cum se va schimba domeniul definiției acestei funcții, dacă vom schimba coeficienții argumentelor și în alte cazuri. Și asta sa întâmplat.
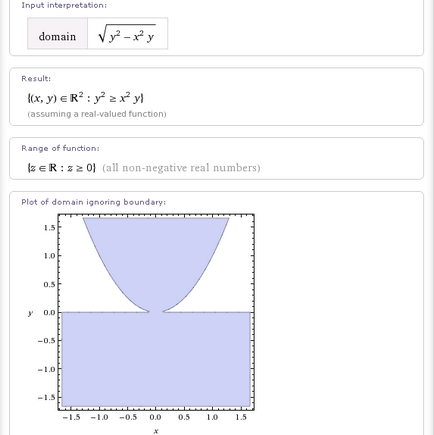
- domeniu sqrt (y ^ 2-x ^ 2y)
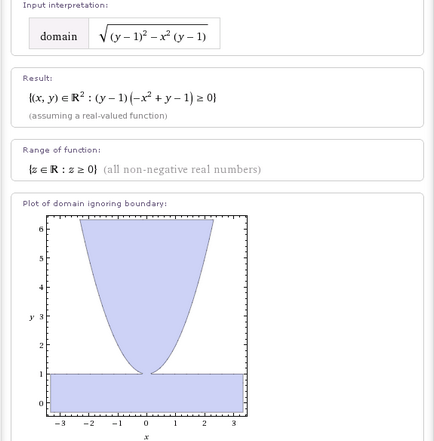
- Domeniul sqrt ((y-1) ^ 2-x ^ 2 (y-1))
- Domeniul sqrt (x ^ 2 (y-1) - (y-1) ^ 2)
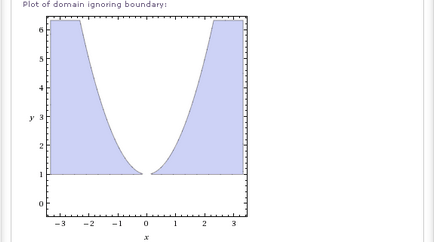
- Domeniul sqrt (x ^ 2y- (y-1) ^ 2 (x-1))
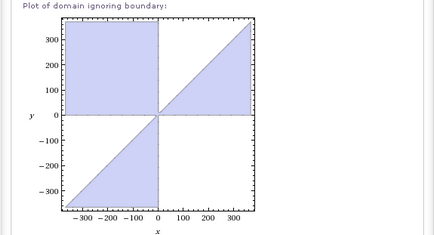
- Domeniul sqrt (-x ^ 2y + (y-1) ^ 2 (x-1))
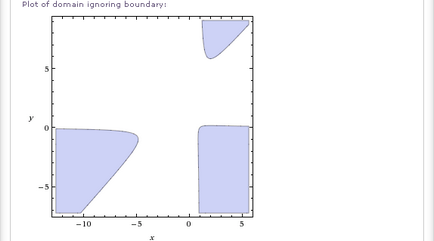
- Domeniul sqrt (sin (y-2) ^ sin (x-2) + sin (x-2) ^ sin (y-2))
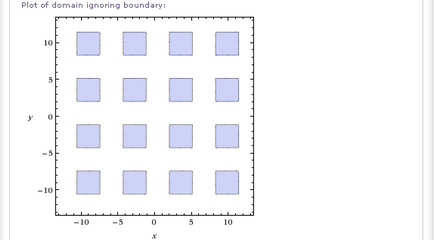
Desigur, există multe alte exemple interesante. Cred că îi veți considera pe cont propriu.
Și, în sfârșit, voi încerca ceva de genul:- Domeniul sqrt (sin (y-2) sin (x-2) + păcat (x-2) sin (y-2)