Clasa 10 "D", liceul BNTU, Republica Belarus, Minsk
Lyakh Alla Saturivna
consilier științific, profesor de matematică, liceu al BNTU, Republica Belarus, Minsk
Pentru funcțiile quadratice date, coeficienții de conducere sunt 1 și -1, adică ramurile ambelor parabole sunt direcționate în direcții diferite. Pentru a determina punctele de intersecție ale grafurilor, se echivă laturile drepte ale ecuațiilor sistemului (⃰⃰) și
Investigăm aranjamentul reciproc al curbelor curbelor date pentru diferite valori ale coeficienților lor și.
1) Dacă. atunci parabolele au două puncte comune.
2) Dacă. atunci parabolele au un punct comun (se ating unii pe alții).
3) Dacă. atunci parabolele nu au puncte comune.
Acum tragem tangente generale la parabole:
Lăsați tangenta comună să atingă parabola într-un punct. și parabolele din punct de vedere (figura 1):
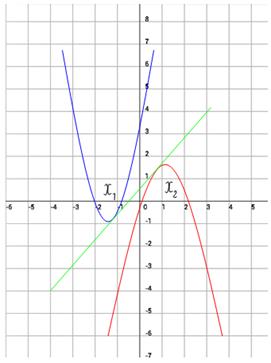
Se scrie ecuația tangentei pentru curbă:
Se scrie ecuația tangentei pentru curbă:
Condiția pentru coincidența completă a două tangente este egalitatea coeficienților corespondenți:
Astfel, avem un sistem de ecuații:
Ca rezultat al transformărilor, obținem ecuația:
1) Dacă. atunci parabolele au două puncte comune și în acest caz este imposibilă trasarea unei tangente comune.
Concluzie: pentru parabolele pentru care coeficienții de conducere sunt 1 și -1 și (parabolele au două puncte comune), nu există o tangență comună.
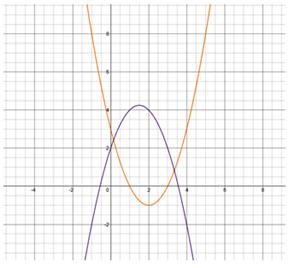
2) Dacă. atunci parabolele au un punct comun (se ating unul pe celălalt) și în acest caz există o singură tangentă comună trasată în punctul de tangență al parabolelor - punctul de tangență.
Ecuația tangentei comune are forma:
Concluzie: pentru parabole, pentru care coeficienții de conducere sunt 1 și -1. (parabolele vor avea un punct comun de tangență), puteți desena o tangență comună în punctul lor de tangență.
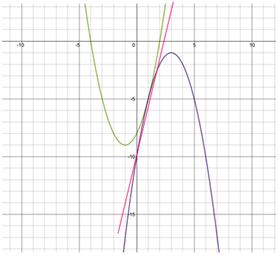
Ecuația tangentei și punctul de tangență:
3) Dacă. atunci parabolele nu au puncte comune și în acest caz putem desena două tangente comune.
Indicați cu A și C punctele de tangență ale grafurilor parabolelor într-un caz, B și D în cealaltă.
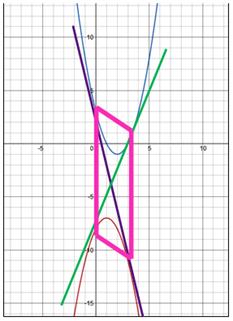
Ecuațiile de tangente comune au forma:
Rețineți că patru puncte de tangență a două tangente comune formează ABCD patrulaterală, în care laturile AB și CD sunt paralele.
Să arătăm că acest patrulater este un paralelogram.
Deoarece coordonatele punctelor M1 și M2 coincid, ABCD cvadrilateral este o paralelogramă.
Concluzie: parabole, ale căror coeficienți de conducere sunt 1 și -1, și (parabolică nu vor avea puncte în comun) pot organiza doua tangente comune, iar punctul de atingere va fi vârfurile unui paralelogram, două laturi paralele cu axa y.
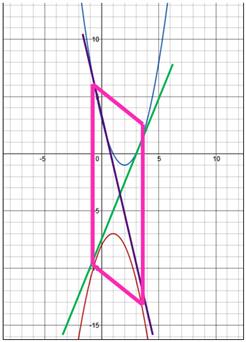
Ecuații de tangente și puncte de tangență:
2. Dicționarul enciclopedic al tânărului matematician. Comp. Savin A.P. M. Pedagogika, 1985. - 352 p .;