ECHIPAMENTE ȘI ACCESORII:
Pendulul, cronometrul, setul de încărcături ale lui Oberbek.
Momentul de inerție al unui punct material cu masa m față de axa de rotație este o cantitate egală cu produsul din masa punctului cu pătratul distanței sale față de axa în cauză:
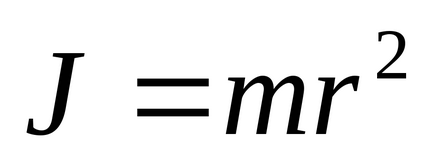
Momentul de inerție al unui sistem de puncte (corp) față de axa de rotație este o cantitate fizică egală cu suma produselor din masele n punctelor materiale ale sistemului pe pătrat de distanțe față de axa examinată:
Teorema lui Steiner. J momentul de inerție în jurul oricărei axe de rotație egală cu momentul de inerție Jc în raport cu axa sa de paralele care trec prin centrul de greutate corporală C, cu produsul pliat asupra greutății corporale și pătratul distanței dintre axe:
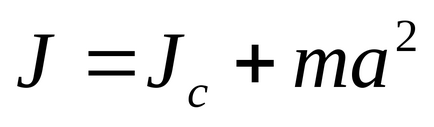
Momentul tăriei
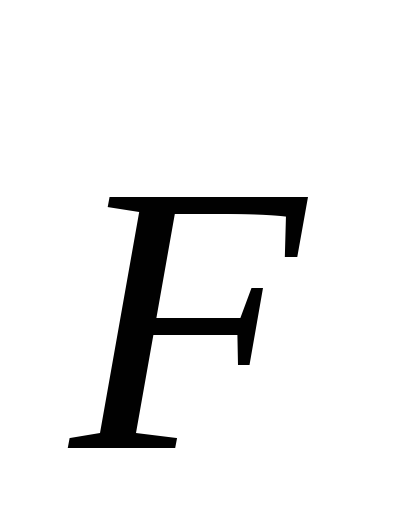
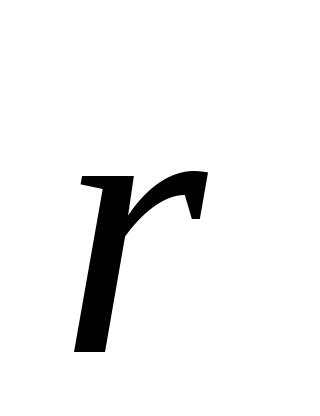
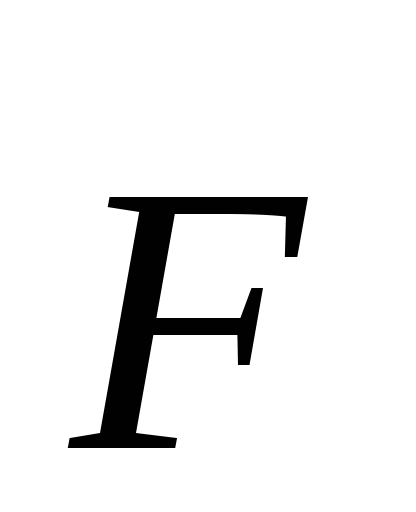
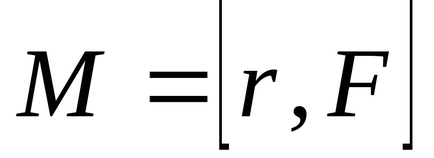
Forțați modulul momentului
Ecuația fundamentală a dinamicii de rotație a mișcării a corpului rigid în raport cu o axă fixă: suma momentelor forțelor care acționează asupra corpului în jurul unei axe, este produsul a momentului de inerție al corpului în raport cu aceeași accelerație unghiulară axă, corpul dobândit
Momentul unghiular
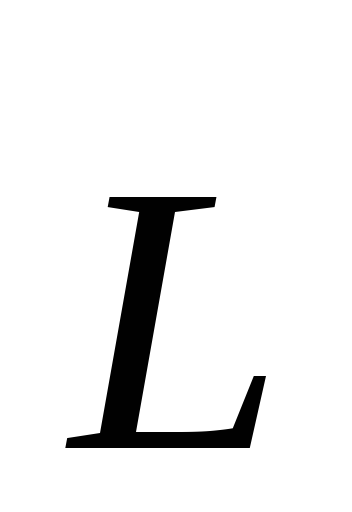
,
Momentul unghiular al unui corp rigid în raport cu axa este suma momentei unghiulare a particulelor individuale:
Având în vedere acest lucru
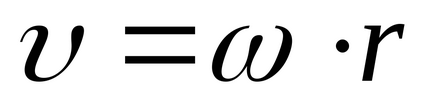
Diferențiezăm ecuația (5) în timp:
Ie ecuația de bază a dinamicii mișcării de rotație a unui corp rigid în raport cu o axă fixă este derivatul momentului unghiular al unui corp rigid față de axa de rotație este egal cu momentul forțelor față de aceeași axă:
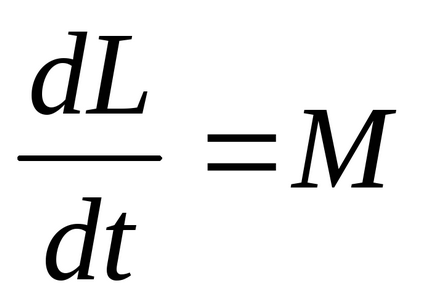
Legea conservării momentului unghiular. Momentul unghiular al unui sistem închis este conservat, adică nu se schimbă în timp
PRINCIPALELE FORMULE DE DESIGN:
Accelerarea încărcăturii:
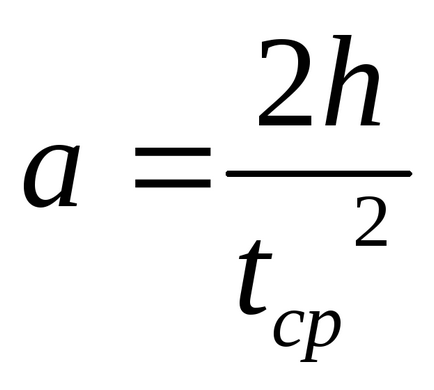
Anglare accelerată:
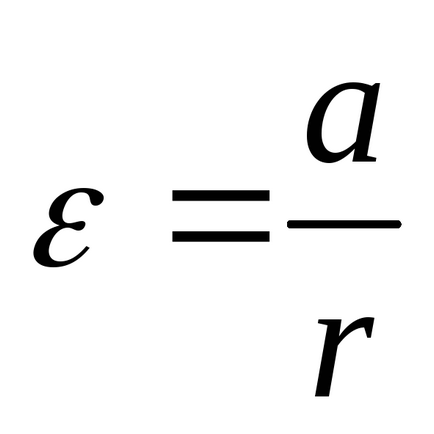
Momentul inerțial al pendulului Oberbeck:
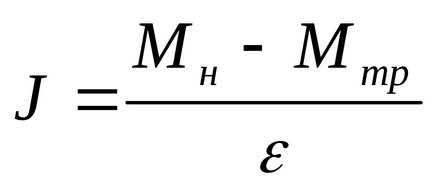
Mtr cuplul de frecare determinate grafic dependența accelerației unghiulare a cuplului care acționează asupra sistemului va fi o linie dreaptă care trece prin punctul [Mtr; 0].