Problema Cauchy pentru ecuația căldurii





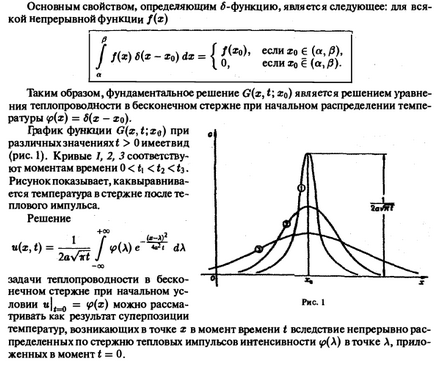
Considerăm că ecuația de căldură omogenă corespunde cazului. lipsa de surse. Problema Cauchy este reprezentată după cum urmează: a găsi o funcție t), care satisface ecuația și condiția inițială a problemei Cauchy pentru ecuația căldurii semnificația fizică a problemei constă în determinarea temperaturii unei tije infinit omogen în orice moment de la temperatura cunoscută a timpului său. Se crede că suprafața laterală a tijei este izolată termic, astfel încât căldura să nu scape din tijă prin ea. M Să presupunem că o funcții suficient de netede ubyvayuyute la x2 + t2 +00 atât de repede încât transformarea Fourier EXISTENT 2) diferențiere legală Apoi, aplicând transformata Fourier pentru ambele părți ale ecuației (1) și condiția (2), de la sarcina (1 ) - (2) trecem la problema Cauchy pentru o ecuație diferențială obișnuită (cantitatea £ joacă rolul unui parametru). Soluția problemei (5) - (6) are forma pe care am stabilit-o mai devreme că, unde este transformarea Fourier a unei funcții. Prin urmare, presupunând t = obține Astfel, poate fi reprezentat ca o parte din stânga a (8) este transformata Fourier a partea dreaptă a ecuației (7) este produsul Fourier transformă funcțiilor folosind teorema convoluția, potrivit căreia egalitatea (7) (argumentul x ) a funcției dorite u (x, t). astfel încât formula (8) poate fi rescrisă ca: unde, formulă folosind expresia funcției sinuozitate 4> (x) R s, am obținut da o soluție a problemei inițiale (1) - (2) este integrala a Poisson. De fapt, este posibil să se demonstreze că pentru orice funcție continuă mărginită IPT), definită prin formula (9), are orice derivate de ordinul cu privire la x și t cu t> 0 și satisface ecuația (1) pentru t> 0 și Vx. Afirmăm că funcția îndeplinește condiția inițială. Am pus Apoi, deci de unde obținem de când Formăm următorul rezultat important. Teoremă 1. În clasa funcțiilor limitate, soluția problemei Cauchy (1) - (2) este unică și depinde continuu de funcția inițială. Un exemplu. Găsiți o soluție la problema problema Cauchy Cauchy pentru ecuația de căldură în timp ce profitând de formula Poisson (9), obținem Proobrazuem integrală privind dreptul de onoare. Trebuie să se schimbe variabilele Apoi intefal partea dreaptă a acestei ecuații ia forma de Formula (I) (Aici am vospoleov inventar pe care le obține că / Prin urmare, soluția la problema limitei și tsya formula Lelia vedea că construit în noiembrie funcția u ( x, f) satisface condiția inițială (2 „). O verificare imediată poate verifica cu ușurință că funitsiya ate la SautWtl ecuație satisface. De la Poisson formula (9) rezultă că etsya rasorosgranya de căldură de-a lungul tijei imediat. Într-adevăr, să presupunem că temperatura inițială) este pozitiv pentru pe zero, și în afara acestui interval. Apoi, pentru distribuția ulterioară a temperaturii, vedem că pentru t> 0 arbitrar și arbitrar mare | x | au tt (x, t)> 0. obyas kyaetsya inexactitate ipoteze teoretice în derivarea ecuația conducției căldurii. care nu iau în considerare mișcarea inerțială a moleculelor. Cu toate acestea, ecuația conductivității termice dă un bun acord cantitativ cu experimentul. O descriere mai precisă a proceselor de transfer termic este dată de așa-numitele ecuații de transfer. 2.1. Soluția fundamentală a ecuației termice Funcția care intră în formula Poisson (9) este numită soluția fundamentală a ecuației de căldură. Considerată ca o funcție a argumentelor x, t, ea satisface ecuația ui = a2uxx, așa cum se poate verifica prin verificare directă. Soluția fundamentală are un înțeles fizic important asociat cu conceptul de puls de căldură. Să presupunem că distribuția inițială a ip (x), temperatura este după cum urmează: Apoi, prin (9), distribuția temperaturii și tija va arata Prin teorema valoarea medie pe care le-am Trecând în această egalitate la limita ca e - * 0, obținem Acest lucru înseamnă că funcţia G (x, t \ ho) este distribuția temperaturii în tija la momentul t> 0, dacă la momentul t inițial = 0 x = xo a avut temperatura la vârf infinit (pentru e - * 0 funcția 4> et; xa) la în diferite valori ale t> Oumeutid (Figura 1). Curbele 1, 2 și 3 corespund punctelor de timp • Figura arată modul în care temperatura din tija este egalizată după impulsul de încălzire. Soluția problemei Cauchy pentru ecuația conducției căldurii problemei conducta de căldură într-o tijă fără sfârșit, cu condiția inițială poate fi considerată ca fiind rezultatul superpoziției temperaturii care apar la punctul x la momentul t, datorită distribuite în mod continuu de-a lungul intensitatea pulsului tija de căldură y> (A) la punctul A, aplicat la momentul t = 0.