Inegalitatea cu privire la media aritmetică și media geometrică (inequality Cauchy)
Media aritmetică a numerelor pozitive n nu este mai mică decât media geometrică.
și egalitatea este atinsă dacă și numai dacă
Un caz special al acestei inegalități, care conectează media aritmetică și media geometrică a două numere pozitive, a fost cunoscut din cele mai vechi timpuri. Cel mai adesea este dovedit folosind o interpretare geometrică.
Construim un cerc cu diametrul AB = a + b.
Din punctul arbitrar C al unui cerc, trageți CD-ul perpendicular pe diametru.
Prin proprietatea unui triunghi cu unghi drept, înălțimea făcută de hypotenuse. este egal cu media geometrică dintre proeminențele picioarelor și hipotenselor:
Conectăm punctul C cu centrul cercului, punctul O. CO este raza, ceea ce înseamnă că acesta este egal cu jumătate din diametru:
adică lungimea CO este egală cu media aritmetică a a și b.
În triunghiul drept, CD-ul COD este un catet, CO este hypotenuse.
Întrucât hypotenuse este întotdeauna mai mare decât piciorul. CO> CD, prin urmare, media aritmeticii a și b este mai mare decât media geometrică a acestora.
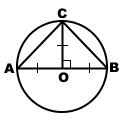
dacă AO = BO, adică a = b.
(de la a> 0), iar în acest caz media aritmetică a a și b este egală cu media geometrică a acestora.
Astfel, media aritmetică a numerelor pozitive a și b nu este mai mică decât media geometrică.
După cum este necesar pentru a dovedi.
În cazul general, inegalitatea a fost dovedită de Cauchy.