1. Forța de frecare alunecătoare
unde este coeficientul de frecare alunecare; valoarea absolută a forței presiunii normale; vector unitate în direcția vitezei corpului.
unde coeficienții de rigiditate;
- coeficientul de rigiditate în raza de conectare a arcurilor cu un coeficient de rigiditate și respectiv;
coeficient de rigiditate cu racordare paralelă a arcurilor cu coeficienți de rigiditate și respectiv; coordonarea capătului liber al arcului; este, de asemenea, pentru izvoare neîngrădite. Semnul minus arată că forța este îndreptată spre lateral, inversul deformării.
unde Nm / kg 2 este constanta gravitationala; ; radius vector al corpului 2 în raport cu corpul 1. Semnul minus indică atracția corpurilor.
unde accelerarea căderii libere (aproape de suprafața Pământului); m / s 2;
unde masa și raza Pământului (planete, stele), respectiv; înălțime deasupra suprafeței Pământului.
5. Principiul superpoziției: În cazul în care un punct material există mai multe forțe, fiecare dintre aceste forțe în funcție de accelerația punctului material în conformitate cu legea a doua a lui Newton, ca și cum ceilalți nu au avut puterea. Conform acestui principiu, forțele și accelerațiile pot fi descompuse în componente. Forța care acționează asupra punctului material care se deplasează de-a lungul curbei poate fi descompusă în două componente - tangențială și normală.
Tangențială (sau tangențială) forță
unde vectorul unității este direcționat de-a lungul tangentei pe traiectorie.
Forța normală (sau centripetală)
unde raza de curbură a traiectoriei; un vector de unitate direcționat de-a lungul traiectoriei normale.
1. Momentul momentului
unde este viteza punctului material.
2. Momentul sistemului de puncte materiale
unde - masa particulei n-a - viteza sa în cadrul inerțial de referință.
Legea a doua a lui Newton
unde suma geometrică a forțelor care acționează asupra punctului material; - impulsul său; este numărul de forțe care acționează asupra punctului.
2. Dacă masa este constantă, noua lege a lui Newton de mecanică clasică poate fi exprimată prin formula
3. Dacă nu este cunoscută exacta lege prin care se schimbă forța totală
acționând asupra corpului, atunci puteți folosi conceptul de rezistență medie pentru o perioadă de timp, de la momentul la.
Apoi ecuația celei de-a doua legi a lui Newton poate fi scrisă în formă
unde este schimbarea momentului în aceeași perioadă de timp; uneori produsul se numește impulsul mediu al forței.
4. A doua lege a lui Newton în forma coordonată (scalară)
unde sub semnul de însumare sunt proiecțiile forțelor pe axele de coordonate corespunzătoare.
A treia lege a lui Newton
unde este forța care acționează asupra punctului material i de la punctul material k; - forța care acționează asupra punctului material k din punctul i material. Forțele care acționează asupra reciproc puncte materiale sunt întotdeauna egale în mărime sunt aplicate la diferite puncte ale materialului, sunt îndreptate în sens opus, întotdeauna funcționează în perechi și acționează de-a lungul unei linii drepte care leagă aceste puncte.
2. Clasificarea sarcinilor și recomandări privind metodele de rezolvare a acestora
Sarcinile dinamicii mișcării rectilinii unui punct material, bazate pe metoda de rezolvare a acestora, pot fi împărțite în următoarele tipuri de bază.
1) Toate forțele. Forțele care acționează pe corp coincid cu linia dreaptă de-a lungul căreia este îndreptat vectorul de accelerare. În acest caz, ecuația celei de-a doua legi a lui Newton în forma vectorială și soluția în formă scalară sunt luate cu atenție pentru direcția forțelor.
2) Dacă forțele care acționează asupra corpului sunt multidirecționale (și chiar mai mult, unele dintre ele nu coincid în direcția c, de exemplu, mișcarea corpului de-a lungul unui plan înclinat):
· Alegeți două axe arbitrare OX și OY (pentru a simplifica soluția, este de dorit să direcționați unul de-a lungul vectorului de accelerație);
· Proiectați toate forțele active pe axa OX și OY;
· Înregistrați a doua lege a lui Newton, respectiv, pentru axele OX:
· Soluiți sistemul de ecuații în comun (dacă este necesar, completați cu ecuațiile cinematice corespunzătoare de mișcare).
3) mișcarea mai multor forțe fire și fara greutate (mișcarea extensibile mai multor organisme de pe planuri orizontale și înclinate asociate; sarcini în blocuri, care este acoperit de un fir - frânghie, frânghie, cordon, etc.).
Principalele regularități în rezolvarea problemelor pe blocuri pot fi formulate după cum urmează:
· Blocul este considerat fără greutate (sau masa acestuia poate fi neglijată);
· Firele între corpurile considerate fără greutate și inextensibile;
· Forțele de tensionare ale filetului de pe ambele părți ale blocului sunt aceleași;
· Legea a doua a lui Newton este redactată separat pentru fiecare organism (luând în considerare direcția aleasă de mișcare a sistemului de corpuri);
· Dacă firul este aruncat, de exemplu, după 2 unitate imponderabil (a - un mobil, al doilea - staționar), tensiunea firului va forța pe întreaga lungime a acestora, dar datorită accelerării traficului unității de marfă mobile este diferit.
3. Exemple de rezolvare a problemelor tipice
Greutatea balon kg M250 a început să scadă cu o accelerație de 0,2 m / s 2. Se determină greutatea balastului, care trebuie resetat la balon primit aceeași accelerație, dar în sus. Accelerația căderii libere este de 9,8 m / s 2. Rezistența la aer este neglijată.
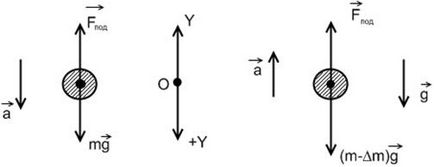
Soluție: Când balonul scade cu accelerație. mai puțin accelerarea căderii libere. și de condiția problemei nu există rezistență la aer, aceasta înseamnă că forța de ridicare acționează asupra acesteia în plus față de gravitate. îndreptată vertical în sus.
Forțele care acționează asupra balonului sunt direcționate vertical, prin urmare, ecuația de mișcare
este suficient să proiectați o singură axă a sistemului de coordonate OY:
De unde vine liftul?
Dacă arunci masa de balast. atunci ecuația de mișcare poate fi scrisă în formă
sau luând în considerare expresia rezultată pentru ascensor
În consecință, masa balastului aruncat este
Masina, pornind de la locul său, accelerează cu o viteză de 72 km / h în decurs de 5 secunde.
Găsiți coeficientul minim de frecare posibil între roțile mașinii și drum în această mișcare.
Care este cea mai mică distanță de frânare a unei mașini care a câștigat această viteză?
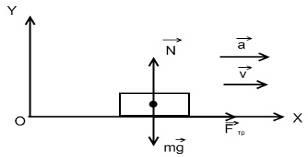
Soluție: Când conduceți o mașină, atât în timpul accelerației, cât și la frânare, trei forțe acționează asupra acesteia: gravitatea. forța unei reacții normale din partea drumului și forța de frecare
a) Când vehiculul este accelerat, forța de frecare previne alunecarea roților motoare de-a lungul suprafeței drumului, deci este îndreptată spre mișcare și este forța de fricțiune de odihnă. În acest caz, forța de frecare va fi forța motrice. Pe baza sistemului de coordonate ales XOY, ecuația de mișcare are forma
În proiecțiile axei sistemului de coordonate:
Exprimând forța de frecare prin forța de reacție și coeficientul de frecare dintre roți și drum
din ecuația de mișcare determinăm accelerația mașinii:
Pe de altă parte, deoarece, din cauza stării problemei, mașina care se deplasează la aceeași viteză a accelerat în timp. atunci accelerarea lui este
Din expresie, avem 0.41. Prin urmare,
b) La frânare, forța de frecare este direcționată în direcția opusă mișcării și este forța de frecare alunecoasă. Ecuația de mișcare a mașinii în acest caz în proiecțiile axelor de coordonate
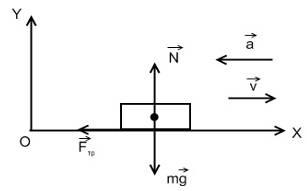
Având în vedere acest lucru. accelerarea mașinii în timpul frânării
Calea traversată de o mașină care se mișcă încet și cu viteza inițială este egală cu
Durata de conducere pentru oprire poate fi determinată de condiția vitezei finale a mașinii
Luând în considerare expresiile pentru coeficientul de frecare (7), obținem
Pe un plan înclinat neted, cu un unghi la bază, există o placă de masă M, iar pe placă se află o bară cu o masă m. Placa este alimentată de o forță îndreptată spre pantă. La ce mărime a acestei forțe se va aluneca sarcina? Coeficientul de frecare dintre placă și bara. Accelerarea căderii libere.
Soluție: forțele care acționează asupra fiecăruia dintre corpurile din cadrul de referință inerțial XOY sunt prezentate în figura 2.4.
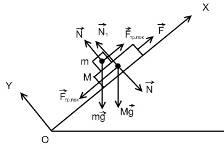
Gravitatea acționează asupra barului. forța de frecare. rezistența și rezistența reacției; Forța gravitațională acționează asupra panoului. forța de reacție. Forța de frecare și greutatea barei sunt egale în mărime. Vom lua în considerare acest lucru
Să scriem a doua lege a lui Newton în proiecțiile axelor sistemului de coordonate ales, cu condiția ca bara să nu alunece pe tablă:
Rezolvăm sistemul de ecuații.
Prin urmare, atunci când bara se îndepărtează de pe placă.
Pe un plan înclinat cu un unghi la bază, un cub se află nemișcat. Coeficientul de frecare dintre pană și cub este. Planul înclinat se mișcă cu accelerație în direcția arătată în Fig. 2.5. La ce valoare minimă a acestei accelerații se va aluneca cubul?
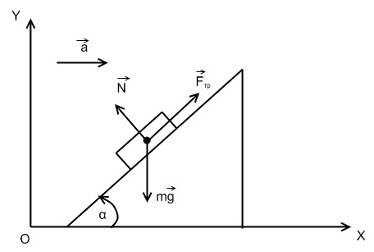
Soluție: Scriem a doua lege a lui Newton în proiecțiile de pe axa x OY și un sistem de referință inerțial, asociată cu Pământul, având în vedere că un cub în raport cu pană se sprijină:
Deoarece cubul este în repaus față de pană, acesta este conectat printr-o relație. și anume
În consecință, când cubul începe să alunece atunci când pană accelerează, egală cu
În cazul în care. atunci corpul va începe să alunece pentru orice accelerare arbitrară mică.