Definiția și formula energiei potențiale
Energia potențială se referă la partea energiei mecanice a unui corp (corp), care depinde de aranjamentul reciproc al părților sistemului (configurației) și poziției în câmpul extern al forțelor.
Energia potențială este determinată de activitatea desfășurată de potențiale forțe care acționează asupra tuturor părților sistemului, în cazul în care sistemul trece de la configurația de test la o stare în care energia potențială este considerată muncă nulyu.A a forțelor conservatoare este egală cu pierderea de energie potențială. Punctul de plecare al energiei potențiale se face arbitrar. Este posibil să se măsoare empiric numai schimbarea energiei potențiale. Punctul de plecare al energiei potențiale se face astfel încât soluția unei anumite probleme să fie simplificată.
Energia potențială este un scalar. Cel mai adesea, energia potențială este desemnată de: Ep, Wp. U.
Energia potențială a sistemului (Ep) poate fi împărțită în energii externe (Ep vnesh) și interne potențiale Ep vnesh. apoi:
unde Ep vnesh este obținut ca urmare a unui impact asupra sistemului din partea corpurilor care nu intră în sistemul în cauză. Ep vnutr - este cauzată de interacțiunea dintre diferite părți ale sistemului constitutiv.
Ep vnutr este o funcție a coordonatelor tuturor punctelor materiale ale sistemului; Ep vnesh, pe lângă coordonate, poate depinde de timp într-o formă explicită.
Expresii pentru energia potențială
Energia potențială a punctului material al forțelor în câmpul potențial este determinată de formula:
unde Y este funcția de forță, C este constanta de integrare.
Forța conservatoare (), care acționează asupra punctului material, este legată de potențiala energie de relația:
unde sau este operatorul hamiltonian (operatorul nabla).
În cazul forțelor conservatoare non-staționare, energia potențială a unui punct material este o funcție a coordonatelor și timpului (Ep = Ep (x, y, z, t)).
Energia potențială internă a sistemului este suma algebrică a energiilor potențiale (Ep (ik)) a interacțiunii tuturor perechilor de puncte ale sistemului:
în cazul în care. - forțele potențiale cu care interacționează punctele i și t din sistem. Dacă corpul este rigid, atunci Ep vnutr = const, atunci se consideră că:
Cazuri particulare de formule pentru potențialele energii
Energia potențială a unui corp deformat elastic pe x este egală cu:
unde k este coeficientul de elasticitate.
Energia punctuală potențială în câmpul gravitațional al Pământului:
unde m este masa unui punct material, M este masa Pamantului, iar R este raza Pamantului. G este constanta gravitationala. Se presupune că energia potențială este zero.
Energia potențială a unui corp ridicat deasupra Pământului la o distanță mult mai mică decât raza Pământului este egală cu:
unde m este masa corpului, g este accelerația datorată gravitației, h este înălțimea ridicării corpului (de la un nivel cu condiție zero, unde se presupune că energia potențială este zero).
Unități de măsură a energiei potențiale
Unitatea de bază pentru măsurarea energiei cinetice (ca orice alt tip de energie) în sistemul SI este J (joule), în sistemul CGS-erg. În acest caz: 1 J = 10 7 erg.
Exemple de rezolvare a problemelor
Sarcină. Punctul material se deplasează în direcția pozitivă a axei X (x> 0) în câmpul forțelor conservatoare, energia potențială a căreia este dată de grafic (figura 1). Cum se va modifica modulul de accelerație în timpul mișcării?
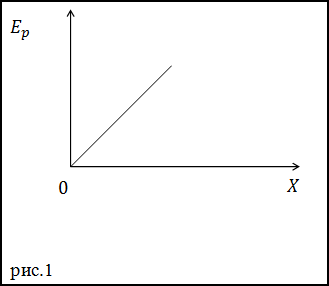
Soluția. Pe baza graficului din figura 1, putem scrie o ecuație care va conecta energia potențială și coordonatele punctului material în timpul deplasării:
unde A este constantă.
Ca bază pentru rezolvarea problemei, folosim formula care relaționează forțele conservatoare și energia potențială:
Pentru mișcarea de-a lungul axei X, care este reprezentată în problema noastră, expresia (1.2) are forma:
În consecință, (1.1) și (1.3), modulul forței care acționează asupra punctului material este egal cu:
Conform celei de-a doua legi a lui Newton, modulul forței poate fi găsit ca:
Prin urmare, obținem o expresie pentru accelerarea punctului material în cauză:
Răspuns. Din expresia obținută pentru accelerarea unui punct material într-un anumit câmp, se poate concluziona că modulo de accelerație nu se schimbă.
Sarcină. Ce se lucra la intensitatea câmpului electromagnetic al punctului material, în cazul în care se mută de particule din coordonatele punctului având (1, 1, 1) la punctul cu coordonatele (2, 2, 2). În acest caz, energia potențială a particulei este dată de funcția :. Rețineți că energia potențială este dată în J, iar coordonatele sunt în metri.
Soluția. Energia potențială este determinată de munca făcută de forțele potențiale, și anume munca forțelor conservatoare este egală cu pierderea energiei potențiale:
Folosind condițiile problemei, găsim Ep1 și Ep2: