
Să începem cu modelul camerei.
Planul de imagine - matrice CCD;
Planul cu vârf - planul unei lentile subțiri;
X este un punct observabil;
f - lungime focală;
Axa optică este axa optică principală.
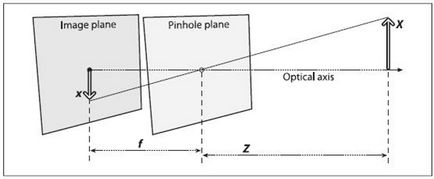
Dacă cineva își amintește cursul de școală al opțiunii geometrice, ecuația de proiecție de perspectivă arată astfel:
Acum, luați în considerare faptul că, de obicei, axa optică principală nu trece prin punctul matricei CCD cu coordonate (0, 0).
Aici c este coordonata punctului de intersecție al axei optice principale a matricei CCD.
Să scriem datele de ecuație pentru coordonatele X și Y, ținând cont de faptul că, datorită erorii tehnologice a procesului de fabricare a matricelor, pixelii au o formă ușor dreptunghiulară.
su și sv sunt factorii de formă pixel.
Noi scriem ecuațiile de proiecție de perspectivă într-o formă de matrice, astfel încât să fie mai convenabil să lucrăm cu ele. Da, și OpenCV sunt prieteni cu matrice.
- coordonatele punctului din sistemul de coordonate exterioare
- coordonatele proiecției punctului
- ecuația matricei de proiecție de perspectivă
Acum ia în considerare faptul că lentila nu este subțire și introduce distorsiune în imagine.
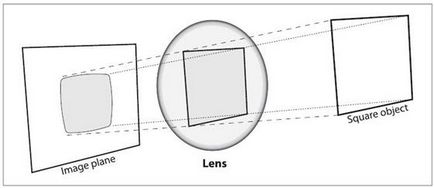
Acest tip de distorsiune se numește radial. Se contabilizează după cum urmează:
Aici r este distanța de la punctul de intersecție al axei optice principale a matricei CCD la punctul de proiecție; k1, k2 sunt coeficienții de distorsiune radială.
Acum, ecuația de matrice a proiecției în perspectivă are forma:
În plus față de distorsiunea radială, există și o distorsiune tangențială. Acest lucru se datorează faptului că planul matricei CCD nu este perpendicular pe axa optică principală. Nu voi lua în considerare modelul: este foarte mic. OpenCV determină și coeficienții de denaturare tangențială.
Când instalați camera, există și erori - vom lua în considerare modelele și ele.
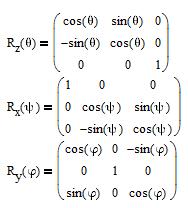
Matricea de rotație rezultată a camerei în jurul sistemului de coordonate cerut:
Vectorul de deplasare al camerei în raport cu sistemul de coordonate cerut:
Acum, modelul camerei, ținând cont de erorile de distorsiune radială și de instalare, arată astfel:
Trecem la coordonatele omogene:
Aici, Rij sunt componentele corespunzătoare ale matricei de rotație a camerei în jurul sistemului de coordonate cerut.
tx, ty, tz sunt componentele vectorului de deplasare a camerei în raport cu sistemul de coordonate cerut.
Așa că am primit modelul camerei.
Acesta include parametrii interni:
fu, fv - lungimi focale
cu, cv - poziția centrului optic
Parametrii externi: 3 unghiuri Euler, 3 componente ale vectorului de traducere.
Și acum să procedăm pentru a defini acești parametri pe OpenCV, adică pentru a calibra aparatul foto.
Principiul de calibrare este foarte simplu - vedem câteva imagini ale tabloului de șah, îi recunoaștem unghiurile. Și știind cum sunt situate colțurile șahului, alegem numeric parametrii camerei. OpenCV are un set de instrumente încorporate pentru a susține un astfel de model de calibrare. Voi folosi interfețele OpenCV pe C ++.