Cum să găsiți zona unui cerc?
Un cerc este o curbă a planului închis, toate punctele fiind la fel de îndepărtate de un punct (centru) dat, situat în același plan ca și curba.
Un cerc face parte dintr-un plan mărginit de un cerc.
Radiusul este un segment al unei linii drepte care leagă centrul unui cerc cu un punct al acestuia, precum și lungimea acestui segment. Este de obicei indicat de R.
Diametrul este un segment de linie dreaptă care conectează o pereche de puncte care sunt cele mai îndepărtate unul de altul, precum și lungimea acestui segment. Diametrul trece întotdeauna prin centrul cercului. Acesta este de obicei marcat cu D sau t. Diametrul este de două ori raza cercului: D = 2R, R = D / 2.
Raportul dintre circumferință și diametru este același pentru toate cercurile. Acest raport este un număr transcendental, notat cu litera greacă pi: π = 3,14159.

Cum de a găsi zona unui triunghi?
Un triunghi este o figură geometrică planificată, mărginită de trei segmente de linii intersectate pereche. Punctele de intersecție nazyvayutsyavershinami treugolinika și desemnat în general cu litere latine majuscule: A, B, C. Velichinyuglov la nodurile din care se intersectează liniile corespunzătoare sunt, de obicei notate cu literele grecești: α, β, y. Opuse colțuri segmente de linie care delimitează nazyvayutsyarebrami triunghi (laturile) ale triunghiului și sunt desemnate respectiv a, b, c.
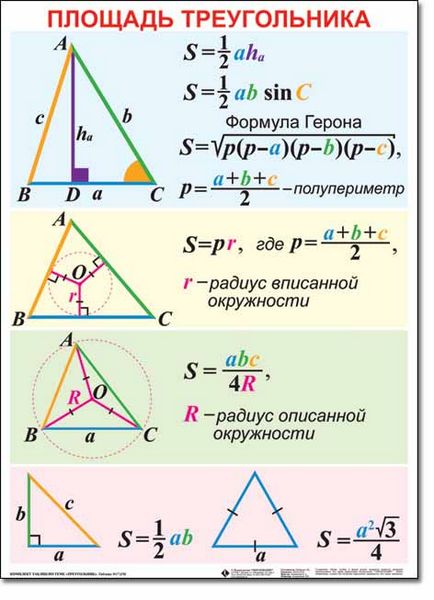
Mai jos sunt formulele prin care puteți găsi zona S a triunghiului cu vârfurile A, B, C, valorile unghiurilor corespunzătoare α, β, γ și laturile opuse a, b, c:
S = a · b · sin (γ) / 2 = a · c · sin (β) / 2 = b · c · sin (α) / 2,
S = a 2 · sin (β) · sin (γ) / (2 · sin (β + γ),
(P - c)) (formula lui Heron), unde √ (.) Este rădăcina pătrată, p = (a + b + c) / 2 Jumătate de perimetru al unui triunghi.
S = a · ha / 2 = b · hb / 2 = c · hc / 2. unde ha este înălțimea căzută de la vârful A la partea a, hb de la vârful B până la partea b, hc de la vârful C până la partea c.
S = r · p. unde r este raza cercului înscris în triunghi, p = (a + b + c) / 2 este semiperimetrul triunghiului.
S = a · b · c / 4R, unde R este raza cercului circumscris în jurul triunghiului.
(. X3 y3) Daca coordonatele carteziene sunt puncte specificate în planul A (. X1 y1), B (. X2 y2) și C, zona S poate fi găsit prin următoarea ecuație (determinantul prin matrici de ordinul doi pentru a coordona diferențele):
S = | (x1 - x3) · (y2 - y3) - (x2 - x3) · (y1 - y3) | / 2. unde |. | | - desemnarea modulului. Această formulă este obținută din expresia pentru produsul vectorial a doi vectori în plan, care este în valoare absolută egală cu valoarea determinantului compus din coordonatele lor.
Cum să găsiți zona unui triunghi drept?
Un triunghi este numit dreptunghi. unul dintre unghiurile cărora este de 90 ° (este drept). Deoarece suma unghiurilor triunghiului este de 180 °, în triunghi poate exista un singur unghi drept.
Mai jos sunt formulele pentru calcularea zonei S. Specific pentru triunghiurile dreptunghiulare. Legenda: c - lungimea hypotenuse (partea opusă unghiului drept), a. b - lungimea picioarelor (laturile adiacente unghiului drept), α. β - valorile unghiurilor opuse acestor picioare (α + β = 90 °).
Pe două picioare: S = a · b / 2
Pe hypotenuse și picior: S = a · sqrt (c 2 - a 2) / 2 = b · sqrt (c 2 - b 2) / 2.
unde sqrt (.) este rădăcina pătrată
Cum pot găsi zona unui pătrat?
Pătratul (din laturile quadratus este patrulateral) este un patrulater obișnuit, cu toate laturile și unghiurile egale. Acesta poate fi definit ca un dreptunghi, în care două laturi adiacente sunt egale unul cu altul, sau ca un romb, în care toate unghiurile sunt drepte.
Simetria. Pătratul are cea mai mare simetrie între toate quadrilaterals. El are:
- patru axe de simetrie de ordinul doi (care pentru figura plane sunt echivalente cu reflecțiile), dintre care două trec de-a lungul diagonalelor pătratului, iar celelalte două - paralele cu laturile;
- o axă de simetrie de ordinul patru (care trece prin centrul pătratului perpendicular pe planul său).
Diagonal. Pătratul are două diagonale care leagă nodurile neasigurate. Diagonalele pătratului sunt bisectoarele unghiurilor sale, se intersectează în centrul pătratului în unghi drept și se împart în fiecare jumătate. Fiecare diagonală împarte pătratul în două triunghiuri dreptunghiulare. Două diagonale împreună împart pătratul în patru triunghiuri dreptunghiulare.
Dacă denotă partea pătratului a. atunci lungimea diagonalei d este calculată de teorema lui Pitagora:
Circuit circumscripționat și circumscripționat. Cercul inscripționat pătrat atinge mijlocul tuturor laturilor pătratului și are o rază r. egală cu jumătatea laturii pătratului a. Cercul circumscris în jurul pătratului trece prin toate vârfurile și are o rază R. egală cu jumătate din lungimea diagonalei pătratului d:
Perimetrul și zona. Perimetrul P al unui pătrat este compus din lungimile celor patru laturi ale acestuia. Zona S a unui pătrat este egală cu pătratul lungimii sale:
P = 4a = 8r = 2√2 · R,
S = a2 = 4r2 = 2R2.
Cum să găsiți zona unui trapez?
Trapezoidul este un patrulater cu două laturi paralele (bazele trapezoidului), iar celelalte două nu sunt paralele (laturile trapezoidale). Segmentul care leagă mijlocul laturilor este numit linia de mijloc a trapezoidului.