Grafice și reprezentarea acestora în memoria calculatorului.
Concepte și definiții de bază ale teoriei grafurilor
Teoria graficelor este o ramură a matematicii care are o aplicație practică largă. În termenii lui, sunt formulate un număr mare de probleme asociate obiectelor discrete. Astfel de probleme apar în proiectarea circuitelor integrate și a circuitelor de comandă, a circuitelor electrice, a diagramelor bloc a programelor, în economie, statistică, chimie, biologie și alte domenii. Teoria grafurilor devine una din părțile esențiale ale aparatului matematic al ciberneticii, limbajul matematicii discrete.
Sarcina 1. Orașul Koenigsberg, situat în Prusia de est, a fost construit la confluența a două râuri pe țărmurile lor și pe două insule. În oraș au existat șapte poduri care au legat insulele între ele și cu părțile de coastă ale orașului (figura 3.1). Este necesar să răspundem la întrebarea: ar putea un rezident din Kenigsberg, care să părăsească casa, să treacă exact toate cele șapte poduri ale orașului și să se întoarcă acasă?
Răspunsul la întrebarea pusă în această problemă ar trebui să fie negativă. Euler a dat acest răspuns și a găsit criteriul existenței unui traseu care să satisfacă cerințele problemei.

Cu toate acestea, rezultatul obținut de Euler a rămas pentru mai mult de o sută de ani singurul rezultat al teoriei grafurilor.
Dezvoltarea teoriei grafurilor la sfârșitul secolului XIX și începutul secolului XX. a fost asociată cu răspândirea ideilor despre structura moleculară a materiei și despre dezvoltarea teoriei circuitelor electrice. Până în anii 50 ai secolului nostru, teoria graficelor a dezvoltat două direcții diferite: algebrice și optimizare.
De exemplu, căutarea unui răspuns la întrebarea prezentată în Problema 1 se referă la direcția algebrică a teoriei grafurilor. Să schimbăm problema 1.
Problema 2. Diferența dintre problema 2 de la sarcina 1 este ceea ce este nevoie pentru a găsi o cale care rezident, a ieșit din casă, va avea loc pe fiecare punte de cel puțin o dată și se va întoarce acasă cu lungimea traseului trebuie să fie minimă.
Sarcina de a găsi un astfel de traseu este legată de direcția de optimizare a teoriei grafurilor.
Oferim definiția unui grafic. Fie V un set non-gol, V setul tuturor subseturilor sale cu două elemente. Perechea (V, E), unde E ÍV este numit grafic (un grafic nedirecționat).
Un grafic este numit finit. dacă setul V este finit. În continuare, termenul "grafic" va însemna grafice finite.
Elementele setului V sunt numite nodurile graficului, iar elementele setului E sunt numite marginile graficului.
Numărul de vârfuri ale graficului G = (V, E) se numește ordinea sa.
Pornind de la definirea unui grafic, fiecare margine corespunde unui subset de două elemente de vârfuri. Dacă subsetul v1, v2> corespunde cu marginea e, atunci spunem că marginea e este incidentă la vârfurile v1 și v2. iar nodurile v1 și v2 sunt adiacente. De asemenea, spunem că marginea e conectează vârfurile v1 și v2. Vitezele v1 și v2 se numesc nodurile terminale ale muchiei e.
Graficul poate fi reprezentat grafic: fiecare vârf este reprezentat de un punct sau de un cerc, iar fiecare margine este reprezentată de un segment care leagă vârfurile finale.
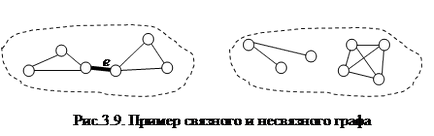
Orice grafic poate fi considerat ca o colecție de grafice conectate. Fiecare dintre aceste grafice este denumită componenta graficului original.
Graficul grafic incoerent prezentat în Fig. 3.9, are două componente.
Setul de arce a căror eliminare din grafic crește numărul componentelor sale se numește tăiere.
Pentru graficul conectat prezentat în Fig. 3.9, tăierea este distanța arc. deoarece îndepărtarea acestuia crește numărul de componente la două.
Să presupunem că G = (V, E), V ¢ÍV, apoi graficul, setul de noduri coincide V ¢, și include o multitudine de arce tuturor pluralitatea nodurilor arc-E terminat în V ¢, numit subgrafic G. concepuți V ¢.
Să presupunem că E ¢ÍE. atunci contorul pentru care o multitudine de arce coincid cu E ¢, iar multimea nodurilor cuprinde arce nodurile incidente ale E ¢, numit un subgraf al lui G, ¢ E concepuți.
Se spune că un grafic este complet dacă două dintre nodurile sale sunt adiacente.
Se spune că un grafic G este gol. dacă nu există muchii în ea.
Un grafic care nu conține cicluri se spune că este aciclic.
Un grafic acyclic nere orientat este numit arbore. un set de copaci este numit pădure.
Dacă marginile care compun un arbore sunt înlocuite de arce orientate, atunci obținem un arbore orientat. Dacă din context este clar ce copac este vorbit, atunci în viitor cuvântul "orientat" va fi omis.
Pentru un copac orientat, este logic să introducem conceptul de rădăcină. Setul minim de vârfuri al unui arbore orientat, din care există căi spre toate vârfurile rămase, se numește setul de rădăcini.
Arborele acoperitor (spanning) al graficului G este un arbore care este un subgraf al graficului G și conține toate vârfurile acestuia.
Dacă graficul G este deconectat, atunci setul constând din arborii de bază ai fiecărei componente se numește pădurea de acoperire (de bază).
Graficul este un hipergraf.
În hipergraf. spre deosebire de un grafic, marginile pot fi nu numai două elemente, ci și orice subset de vârfuri.
Obiecte asemănătoare în matematică sunt cunoscute de mult timp, însă introducerea termenului "hipergraf" este asociată cu luarea în considerare cu succes a unui număr de concepte și metode importante ale teoriei de grafic pe ele.
3.1.2. Prezentarea graficelor în memoria calculatorului
Orice grafic poate fi reprezentat în formă de matrice.
Pentru graficul prezentat în Fig. 3.5, matricea de contiguitate este prezentată în Tabelul 3.1.
Rețineți că pentru graficele ne-orientate, matricea de adjacență este simetrică față de diagonala principală, adică este suficient să se păstreze doar jumătate din matrice în memoria calculatorului.
Matricea de adjunctă a graficului prezentată în figura 3.5
În practică, foarte des matricile reprezentând grafice sunt foarte evacuate, adică conțin multe simboluri "0" sau "¥". Acest lucru duce la costuri nejustificate ale memoriei atunci când se stochează aceste matrice pe un computer.
Cantitatea de memorie poate fi redusă semnificativ dacă matricile sunt împachetate în liste de tip imbricate.
Un exemplu de ambalare a matricei considerate de greutăți (tabelul 3.3) în lista tipurilor de cuiburi implementate pe trei vectori (tablouri) este prezentată în figura 3.10.
Pentru a găsi vârfurile adiacente vârfului i și greutățile arcurilor corespunzătoare din această structură, este necesar să se calculeze indicele inițial In și final Ik în vectorii V și S prin formule
Pentru a stoca matricea de greutăți atât de împachetate, avem nevoie de 42 de celule de memorie ocupate de matricele V, S și U. Matricea neambalată ocupă 10'10 = 100 celule de memorie.
Ris.3.10. Ambalarea matricei de greutăți (tabelul 4.3) în lista tipului imbricat
Când se implementează algoritmi în care se modifică graficul inițial (se adaugă sau se elimină nodurile etc.), este uneori convenabil să se folosească liste de adjacență pentru a stoca grafice. Lista de adiacențe poate fi implementată prin crearea unei liste liniare de liste liniare n, unde n este numărul de vârfuri ale graficului.
Pentru graficul prezentat în Fig. 3.7, lista de adjacități este prezentată în Fig. 3.11.

O altă modalitate de a stoca grafice este o listă de margini, adică o listă în care sunt enumerate toate marginile graficului.
Lista de margini ale graficului prezentată în Fig. 3.7, este prezentat în Fig. 3.12.
Lista margini este realizată pe trei tablouri și ocupă 48 de celule. De asemenea, puteți utiliza structuri de listă în loc de tablouri.
Alegerea acestei sau acelei metode de codificare grafică și structura de date pentru implementarea acesteia depinde atât de sarcina specifică, cât și de algoritmul pentru soluția sa, datele posibile de intrare și de înclinațiile individuale ale programatorului.