Grafice de funcții
Cu toate că pe examenul însuși ne așteptăm să lucrăm cu graficele funcțiilor, totuși, în unele sarcini, li se oferă descrieri în locul cifrelor. Acest lucru este făcut pentru a sublinia acele detalii pe care ar trebui să le acordați atenție atunci când lucrați cu grafice funcționale.
Sarcina numărul 5 este simplă, totuși ultimele sarcini sunt gândite în așa fel încât elevii curioși au avut de gând să se gândească.
Răspunsul din sarcina 5 este un set de cifre care descriu corespondența dintre diferite obiecte.
Teoria pentru sarcina numărul 5
Deoarece în această sarcină vorbim despre funcții și graficele lor, le dăm conceptele și formulele de bază.
Pe un exemplu arbitrar, să examinăm funcția:
- domeniu și set de valori
- rădăcinile și punctele critice
- intervale de scădere în creștere
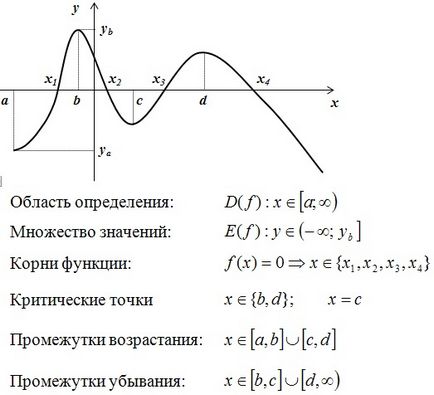
Acum, luați în considerare acest material pe o funcție liniară:
unde k este panta, b este termenul liber
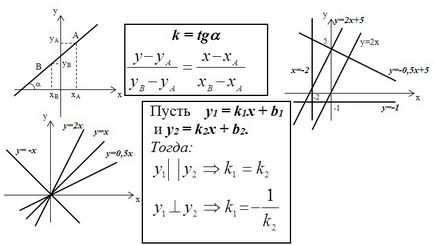
Luați în considerare cazul unei funcții patrate:
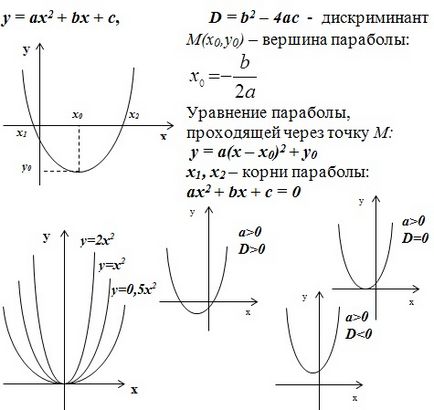
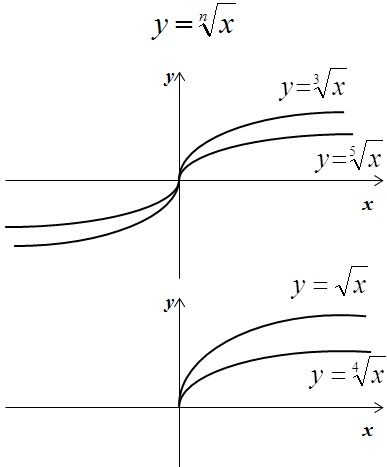
Am analizat trei cazuri - cazul cu o parabolă și efectul coeficienților asupra vederii parabolice - în primul exemplu. În cel de-al doilea exemplu, sunt analizate hiperbola și modelele generale ale dependenței formei generale a graficului de expresia matematică. Cel de-al treilea caz are în vedere direcțiile și variantele sale de construcție în funcție de coeficienți.
Analiza variantelor tipice ale sarcinii №5 a OGE privind matematica
Prima variantă a sarcinii (parabola)
Cifrele arată grafice ale funcțiilor formularului
Stabiliți o corespondență între semnele coeficienților a și c și graficele funcțiilor.
A) a> 0, c> 0
B) a <0, c> 0
B) a> 0, c <0
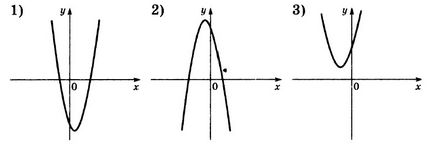
Ne amintim ce corespund coeficienții a și b atunci când construim grafice ale unei funcții a formei
Coeficientul a determină direcția ramurilor parabolei: dacă a> 0, atunci ramificațiile sunt îndreptate în sus și dacă o <0, то ветви направлены вниз.
Astfel, vedem că numai în cea de-a doua parabolă ramurile sunt îndreptate în jos, deci a <0.
Prima și a treia ramură sunt direcționate în sus, adică,> 0.
Apoi ne uităm la ceea ce influențează coeficientul c.
Coeficientul c este responsabil pentru poziția parabolei în raport cu axa x sau este responsabil pentru schimbarea axei y, și anume:
dacă c> 0, atunci vârful parabolei se află deasupra axei x
dacă c <0, то вершина параболы расположена ниже оси x
Astfel, în prima parabolă c <0, у второй и третьей c> 0.
Din toate cele de mai sus, puteți găsi răspunsul:
A doua variantă a sarcinii (hiperbolă)
Se potrivesc funcțiile și graficele acestora.
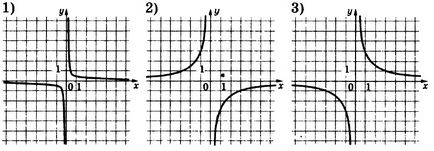
În această situație, puteți utiliza două abordări - puteți fi ghidată de considerente generale sau pur și simplu puteți rezolva problema prin înlocuire. Vă recomandăm să rezolvați problema prin considerații generale și să verificați prin înlocuire.
- dacă ecuația hiperbola este pozitivă (adică, nu există nici un semn - ca în al doilea și al treilea caz), atunci graficul funcției constă în primul și al treilea trimestru de coordonate
- dacă înainte de ecuația hiperbolă există un semn - (ca în primul caz), atunci graficul se află în al doilea și al patrulea trimestru
Astfel, putem determina imediat că prima ecuație corespunde graficului sub numărul 2.
A doua regulă pe care o folosesc este:
- Cu cât este mai mare numărul din numitorul hiperbola (lângă x), cu atât clemele de hiperbolă sunt mai puternice față de axele planului de coordonate
- Cu cât este mai mare numărul în numerotatorul ecuației hiperbolice, cu atât este mai slab și mai lent graficul funcției este apăsat pe axe
În consecință, funcția B este mai slabă față de axe și corespunde graficului 3, iar funcția B corespunde graficului 1, deoarece este mai presat la axe.
A treia variantă a sarcinii (graficul de linie)
Se potrivesc funcțiile și graficele acestora.
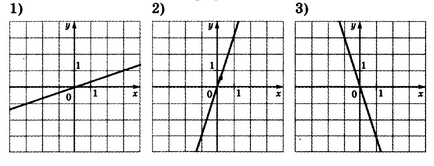
Funcția este o relație liniară, și anume ecuația de ordinul întâi al formei:
Graficul funcției depinde de k și b.
- dacă k <0, то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
- dacă k> 0, atunci funcția crește, adică linia merge de jos în sus, ca și în primele două cifre
- coeficientul b determină schimbarea axei y, dacă b <0, то прямая пересекает ось y ниже 0 в точке y = b, если b> 0, apoi peste zero în punctul y = b
- dacă k> 1, atunci linia merge mai abruptă decât cea uzuală y = x (ca în graficele al doilea și al treilea), dacă k <1. то положе, как на примере рисунка №1
Prin urmare, graficul y = 3x corespunde cu figura 2, deoarece linia merge de jos în sus și este mai abruptă decât curba din figura 1, la care corespunde funcția y = (1/3) x.
Graficul 3 corespunde funcției y = -3x, deoarece k = -3 <0, и график идет сверху вниз.
În cea de-a cincea sarcină a versiunii demonstrative a OGE privind matematica, suntem întrebați despre următoarele:
Se potrivesc graficele funcțiilor cu formulele care le definesc.
Pentru a rezolva această problemă este necesar să se cunoască forma grafurilor de funcții, și anume:
y = x2 este o parabolă, în general este y = ax2 + bx + c, dar în cazul nostru b = c = 0 și a = 1
x / 2 este o linie dreaptă, în general graficul liniei are forma y = ax + b, în cazul nostru b = 0, a = 1/2
y = 2 / x este o hiperbola, în general graficul funcției y = a / x + b, în acest exemplu b = 0, a = 2
Parabola este prezentată în figura A, hiperbola în figura B, iar linia dreaptă este B.