Mișcarea de-a lungul cercului este numită uniformă dacă valoarea vitezei rămâne neschimbată.
Principalele caracteristici ale acestei mișcări sunt:
• raza cercului R;
• viteza (viteza liniară) V;
• viteza unghiulară de mișcare;
• unghiul de rotație al razei (deplasare unghiulară)
Viteza unghiulară a unui corp care se deplasează uniform în jurul circumferinței este raportul dintre unghiul de rotație al vectorului său de rază și timpul de rotație:
În fizică, se folosește o măsură radiantă a unghiului (fără dimensiuni), care este definită ca raportul dintre lungimea arcului (l) și raza
cerc :. astfel încât dimensiunea vitezei unghiulare -
. Fig. 3.19, a. Radian - un unghi a cărui lungime a arcului este egală cu raza cercului. O întoarcere completă într-un cerc conține 2π radiani.
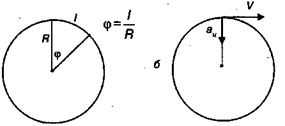
Fig. 3,19. Măsurarea radiană a unghiului (a). Accelerarea prin centrifugă (b)
Între viteze lineare și angulare există o legătură simplă:
Se poate arăta (figura 3.19.6) că, pentru mișcarea uniformă de-a lungul circumferinței, vectorul de accelerație este îndreptat spre centru. Această accelerație se numește centripetal.
Amplitudinea accelerației centripetale este dată de formule
În plus față de caracteristicile de bază ale mișcării de rotație, se folosesc următoarele cantități auxiliare:
• viteza (v), egală cu numărul de rotații pe unitate
timp: (N - număr de rotații). Dimensiunea este de 1 / s.
• perioada de revoluție (T), egală cu timpul pentru care corpul face o revoluție :. Dimensiune - cu.
Aceste mărimi sunt legate de viteza unghiulară prin relațiile:
Mișcare neuniformă de-a lungul unui cerc
Dacă viteza corpului care se deplasează de-a lungul circumferinței se schimbă în magnitudine, atunci, împreună cu accelerația centripetală la, va avea loc și accelerarea tangențială la. Fig. 3.20.
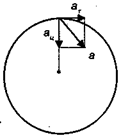
Fig. 3.20. Elemente de accelerare pentru mișcarea rotativă neuniformă
Spre deosebire de accelerația centripetală, care se datorează unei schimbări în direcția vitezei, accelerația tangențială se datorează unei modificări a mărimii vectorului de viteză:
Accelerația tangențială este întotdeauna îndreptată de-a lungul tangentei către cerc, iar dacă viteza crește, direcția sa coincide cu direcția de mișcare. Dacă viteza scade, direcția accelerației tangențiale este opusă vectorului de viteză. Vectorii a, și un # 964; sunt perpendiculare unul pe altul, iar suma lor dă vectorul accelerației totale:
Deoarece aceste vectori sunt întotdeauna perpendiculare una cu alta, magnitudinea accelerației totale în orice moment este:
Cu accelerația tangențială, ne întâlnim în sport. De exemplu, atunci când ciocanul este dezbrăcat, sportivul îl informează despre accelerația tangențială pentru ca acesta să obțină o viteză mare la momentul turnării.
În plus față de accelerația obișnuită (a). când se descrie mișcarea neuniformă de-a lungul circumferinței, se utilizează încă o caracteristică - accelerația unghiulară (# 949;).
Accelerația unghiulară a unui corp este derivată din viteza unghiulară în raport cu timpul (raportul dintre variația vitezei unghiulare și timpul acestei modificări, calculat într-un interval foarte mic al unui punct dat al traiectoriei):
Accelerarea în SI este 1 / s 2.
Notă. În acele cazuri în care viteza unghiulară este privită ca un vector, accelerația unghiulară este, de asemenea, un vector. În acest manual, astfel de cazuri nu sunt luate în considerare.
Se poate demonstra că accelerația unghiulară este egală cu raportul dintre accelerația tangențială și raza cercului: