Acum ne vom da seama cum să găsim zona unui triunghi printr-un cotangent sau, mai precis, să luăm în considerare derivarea unei formule. Cum arată aria triunghiului atunci când se calculează prin cotangență? Aici.
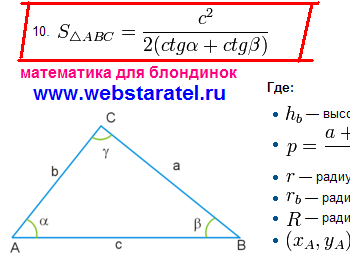
Știm cu toții că aria triunghiului este egală cu jumătate din produsul bazei până la înălțime. Unde merge înălțimea și unde apar cotangentele în această formulă? Cum se obține această formulă? Rețeta este destul de simplă, ca și în gătit. Trebuie să luăm componentele necesare ale acestei mâncăruri matematice, să le pregătim mai întâi și să pregătim formula din produsele semifinite. Produsele alimentare pe care le cumpărăm în magazin. Unde să luați componentele unei formule matematice? Triunghiul pe care-l avem deja. De asemenea, avem nevoie de definirea unui cotangent printr-un triunghi. Facem o fotografie pe pagina specificată și decupăm componentele necesare.

Acum începe lucrarea de pregătire preliminară pentru procesul de derivare a formulei. Ca și în bucătărie, trebuie să pregătiți totul în mod corespunzător - curățați, tăiați, prăjiți, fierbeți. Pe scurt, știi mai bine decât mine ce să faci în bucătărie. Pot mânca numai.
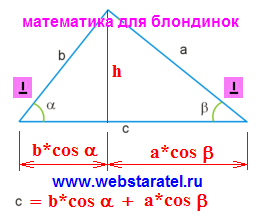
Ștergem din imagine tot ceea ce este de prisos. În roșu, am dorisoval de ce avem nevoie. Înălțimea triunghiului intră în zona triunghiului. Se împarte baza în două segmente. Lungimea fiecărui segment este definită ca proiecția pe baza de deasupra laturii triunghiului. Folosind un portret al unei tangente. Pot să determin cu ușurință că trebuie să folosiți cosinele colțurilor. Se scrie formula bazei ca suma a două proiecții ale laturilor. Trecem la imaginea cotangentei.
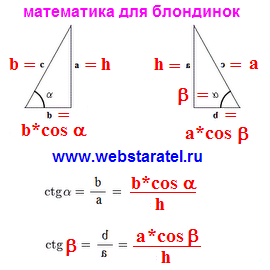
Acum, din imaginea triunghiului, trebuie să transferăm toate notațiile la imaginea cotangentă. Cu colțul din stânga, nu există nici o problemă, în ambele imagini sunt îndreptate într-o singură direcție. Folosind notația veche în formula cotangent și semnul egal pe imagine, obținem cu ușurință formula cotangentă a unghiului alfa pentru triunghiul nostru. Dar cu un unghi beta au existat mici probleme. El privește în sens invers. Nu dispera. Ca comenzi reale, luați o imagine cu un unghi alfa și efectuați operația "cu fața în jos", adică o punem cu fața la podea. Am pus cătușe pe ea și l-am adus la fereastră. Printr-o foaie de hârtie apare un model vag. Wow! Da, acesta este același unghi de care avem nevoie! Și pretinzând că este un unghi diferit (în rețete nu veți găsi astfel de receptoare, dar la urma urmei, matematica nu gătește). Puneți notația noastră pe imaginea inversată și obțineți valoarea cotangentului unghiului beta.
Asta e tot. Acum începem să pregătim antena însăși, adică să deducem formula de zonă a triunghiului prin cotangentele celor două unghiuri α și β. Repet că începem cu formula generală, unde aria triunghiului este egală cu jumătate din produsul bazei până la înălțime. Înregistrăm totul separat: jumătate, fund și înălțime. Apoi, cu înălțimea, începem să realizăm transformări magice în strictă conformitate cu formulele pe care le-am primit deja.
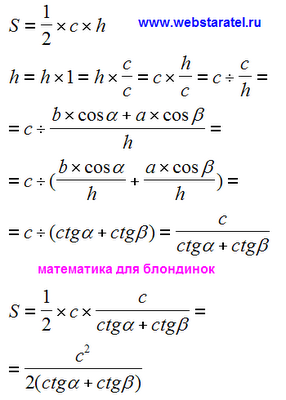
În final, valoarea înălțimii triunghiului, exprimată prin cotangent, este înlocuită în prima formulă și o transformăm într-o grămadă. După cum puteți vedea, nu este nimic dificil în această rețetă.
O recomandare generală pentru derivarea altor formule. Vedeți ce aveți la început și la sfârșit. Căutați ceva ce poate fi legat împreună. În cazul nostru, începutul și sfârșitul sunt legate de definiția cotangentului prin triunghi.