Integrarea numerică este o operație computațională destul de simplă. Este implementat sub forma operatorului corespunzător MathCAD. Rezultatul integrării numerice este un anumit număr - valoarea unui integrat definit.
Pentru a calcula un integral integrat, trebuie să-i scrieți forma obișnuită matematică:
Rezolva un integral definitiv prin următoarele metode aproximative:
Ideea principală a acestei metode se bazează pe considerente geometrice simple, și anume un integral definitiv, care este zona trapezoidului curbilinar. Se calculează ca suma suprafețelor de dreptunghiuri elementare.
Metoda dreptunghiurilor stângi
Segmentul integratului este împărțit în segmente n-elementare de lungime egală.
Un exemplu al metodei dreptunghiurilor stângi din Figura 7.
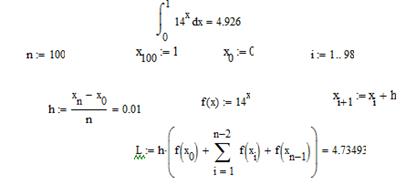
Fig. 7. Metoda dreptunghiurilor stângi.
Drept dreptunghi.
Segmentul integratului este împărțit în segmente n-elementare de lungime egală
Un exemplu al metodei dreptunghiurilor drepte din Figura 8.
Fig. 8. Metoda dreptunghiurilor drepte.
Metoda de dreptunghiuri medii
Segmentul integratului este împărțit în segmente n-elementare de lungime egală
Un exemplu de metodă a dreptunghiurilor medii din Figura 9.
În metoda trapezoidală, elementele trapezoidale curvilineare sunt înlocuite cu trapezii dreptunghiulare, rezultând o modalitate aproximativă de a găsi un integrat definit.
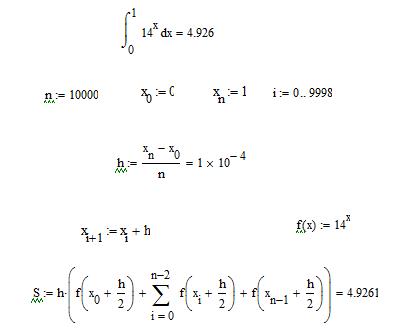
Fig. 9. Metoda dreptunghiurilor medii.
Exemplul metodei trapezoidale din figura 10.
Fig. 10. Metoda trapezului.
În această metodă, segmentul integralului nu este divizat în n segmente elementare, ci în n perechi de segmente elementare.
Un exemplu al metodei Simpson din Figura 11.

Capitolul 2. Metode de rezolvare a ecuațiilor neliniare
Toate funcțiile care nu sunt algebrice sunt numite transcendentale (neliniare). Toate metodele considerate pentru rezolvarea ecuațiilor algebrice neliniare sunt proceduri iterative care rafinate secvențial valoarea rădăcinii prin intermediul unei anumite algoritmi sau formula de iterație.
Să fie abscisele capetelor coardei, să fie ecuația liniei drepte care conține coarda. Gasim coeficientii u din sistemul de ecuatii:
Se scade din prima ecuație a doua:
. atunci vom găsi coeficienții u:
Ecuația ia forma:
Astfel, putem gasi prima aproximatie la radacina obtinuta prin metoda chordului:
Acum, luați coordonatele și repetați toate operațiile efectuate, găsind o nouă aproximație la rădăcină. Repetați operația până când aceasta este mai mică sau egală cu valoarea de eroare specificată.
Un exemplu de metoda acordurilor din figura 12.
