Funcțiile și recursul în C ++

Ei bine, sărbătorile de Anul Nou au ajuns la sfârșit, și cu ei antrenamentul meu în C ++. După cum a spus, a absolvit cu onoruri. Astăzi vom lua în considerare sarcinile care utilizează funcții. O parte din sarcini vor fi rezolvate folosind funcții recursive. Permiteți-mi să vă reamintesc că aceste sarcini au fost luate în considerare în cursul Introducere în programare (C ++) pe site-ul steptic.org. Acum voi împărți niște știri și apoi vom începe sarcinile.
Un pic îmbunătățit site-ul
Scrieți funcția min (a, b). care calculează minimul de două numere. Apoi scrieți funcția min4 (a, b, c, d). calculând un minim de 4 numere folosind funcția min. Numără patru numere întregi și le scoate cel puțin.
Formatul de intrare
Se introduc patru numere întregi.
Formatul de ieșire
Realizați răspunsul la sarcină.
Se dau patru numere reale: $% x_1 $%, $% y_1 $%, $% x_2 $%, $% y_2 $%. Scrieți funcția de distanță (x1, y1, x2, y2). care calculează distanța dintre punctul $% (x_1, y_1) $% și $% (x_2, y_2) $%. Citiți cele patru numere reale și scoateți rezultatul acestei funcții.
Formatul de intrare
Sunt introduse patru numere reale.
Formatul de ieșire
Realizați răspunsul la sarcină.
Două numere reale $% x $% și $% y $% sunt date. Verificați dacă punctul cu coordonatele $% (x, y) $% aparține pătratului umbrit (inclusiv limita acestuia). Dacă punctul aparține unui pătrat, imprimați cuvântul DA. altfel imprimați cuvântul NO.
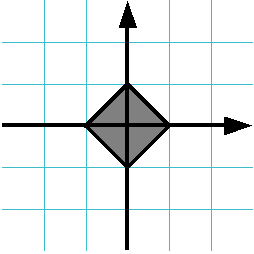
În figură, grila este desenată în pași de 1.
Soluția trebuie să conțină funcția IsPointInSquare (x, y). care se întoarce adevărat. dacă punctul aparține unui pătrat și fals. dacă nu aparține. Programul principal ar trebui să citească coordonatele punctului, să apeleze funcția IsPointInSquare și, în funcție de valoarea returnată, să afișeze mesajul dorit.
Funcția IsPointInSquare nu trebuie să conțină o instrucțiune if.
Formatul de intrare
Două numere reale sunt introduse.
Formatul de ieșire
Realizați răspunsul la sarcină.
Cinci sunt numere reale: $% x $%, $% y $%, $% x_c $%, $% y_c $%, $% R $%. Verificați dacă un punct aparține $% (x, y) $% cerc centrat $% (x_c, y_c) $% și raza $% r $%. Dacă punctul aparține unui cerc, imprimați cuvântul DA. altfel imprimați cuvântul NO.
Soluția trebuie să conțină funcția IsPointInCircle (x, y, xc, yc, r). care returnează True. dacă punctul aparține cercului și False. dacă nu aparține.
Programul principal trebuie să citească coordonatele punctului, să apeleze funcția IsPointInCircle și, în funcție de valoarea returnată, să afișeze mesajul solicitat.
Funcția IsPointInCircle nu trebuie să conțină o instrucțiune if.
Formatul de intrare
Sunt introduse cinci numere reale.
Formatul de ieșire
Realizați răspunsul la sarcină.
Verificați dacă punctul acestei zone umbrite aparține:
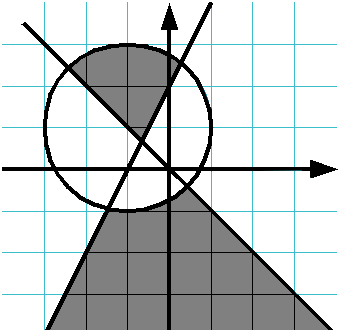
Dacă punctul aparține regiunii (zona include limitele), scoateți cuvântul DA. altfel imprimați cuvântul NO.
Soluția trebuie să conțină funcția IsPointInArea (x, y). care returnează True. dacă punctul aparține domeniului și False. dacă nu aparține. Programul principal trebuie să citească coordonatele punctului, să apeleze funcția IsPointInArea și, în funcție de valoarea returnată, să afișeze mesajul necesar.
Funcția IsPointInArea nu trebuie să conțină o instrucțiune if.
Formatul de intrare
Două numere reale sunt introduse.
Formatul de ieșire
Realizați răspunsul la sarcină.
Având un număr real pozitiv $% a $% și un număr întreg $% n $%. Calculați $% a ^ n $%. Soluția este concepută ca o funcție a puterii (a, n).
Formatul de intrare
Se înregistrează un număr real pozitiv $% a $% și un număr întreg $% n $%.
Formatul de ieșire
Realizați răspunsul la sarcină.
Având un număr natural $% n> 1 $%. Ieșiți cel mai mic divizor, altul decât 1.
Soluția este concepută ca o funcție MinDivisor (n). Numărul de operații din program trebuie să fie proporțional cu $% sqrt $%.
indicație
Dacă numărul $% n $% nu are un divizor mai mic de $% n $%. atunci numărul $% n $% este prim și răspunsul este numărul $% n $%.
Formatul de intrare
Se introduce un număr natural.
Formatul de ieșire
Realizați răspunsul la sarcină.
Având un număr natural $% n> 1 $%. Verificați dacă este simplu. Programul ar trebui să afișeze cuvântul DA. dacă numărul este prime și NO. dacă numărul este compus.
Soluția este concepută ca o funcție IsPrime (n). care returnează True pentru numerele prime și False pentru numerele compuse. Numărul de operații din program trebuie să fie proporțional cu $% sqrt $%.
Formatul de intrare
Se introduce un număr natural.
Formatul de ieșire
Realizați răspunsul la sarcină.
Puteți să o faceți mult mai repede decât multiplicările $% n $%! Pentru a face acest lucru, trebuie să utilizăm următoarele relații de recurență:
$% a ^ n = (a ^ 2) ^ $%, pentru un eveniment $% n $%
$% a ^ n = a × a ^ $%, pentru un impar $% n $%
Implementați un algoritm de exponentizare rapidă cu ajutorul unei funcții recursive.
Formatul de intrare
Se introduce un număr real a și un număr întreg nonnegative $% n $%.
Formatul de ieșire
Realizați răspunsul la sarcină.
Numărul sarcinii 10
Având o secvență de numere, terminând cu numărul 0. Găsiți suma tuturor acestor numere fără a utiliza un ciclu.
Formatul de intrare
Introduceți o secvență de numere întregi, terminând cu un număr 0 (numărul 0 în sine nu este inclus în secvență, ci servește ca semn al sfârșitului acestuia).
Formatul de ieșire
Realizați răspunsul la sarcină.
Numărul sarcinii 11
Scrieți funcția fib (n). care pentru un anumit număr întreg nonnegative $% n $% returnează $% n $% - e numărul Fibonacci. În această sarcină, nu puteți folosi buclele - utilizați recursivitatea.
Primul și al doilea numere Fibonacci sunt egale cu 1, iar fiecare următor este egal cu suma celor două precedente.
Formatul de intrare
Se introduce un număr întreg.
Formatul de ieșire
Realizați răspunsul la sarcină.
Numărul sarcinii 12
Având în vedere numărul N. Se determină numărul de moduri în care pot fi aranjate pe bord $% N x N $% $% $% N regine fără a lovit reciproc.
Formatul de intrare
Se dă un singur număr $% N $%. $% (N ≤ 10) $%
Formatul de ieșire
Realizați răspunsul la sarcină.