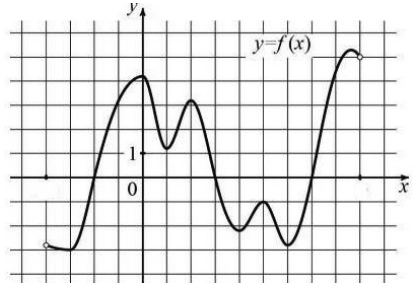
Fig. 1. Graficul grafic al funcției $ y = f (x) $.
Diagrama pentru plotarea unei funcții
- Domeniul $ D (f) $ și domeniul $ E (f) $.
- Paritatea ($ f \ stânga (x \ dreapta) = f \ stânga (-x \ dreapta)) $, $ f \ stânga (x \ dreapta) = f \ stânga (x + T \ dreapta)) $.
- Puncte de intersecție cu axele de coordonate și intervalele în care $ f \ left (x \ right)> 0 $ și $ f \ left (x \ right)
- Pentru a investiga prin creșterea $ '\ left (x \ right)> 0) $, scăderea $' \ left (x \ right)
- Pentru a studia punctele de inflexiune și intervalele de convexitate $ (f ^ \ left (x \ right)> 0) $, concavitatea ($ f ^ \ stânga (x \
- Calculați limitele la limitele domeniului de definiție.
- Valorile în puncte suplimentare.
- Program.
Reguli pentru plotare
- $ Y = f (x-a) $ obținută din grafic $ f (x) $ muta axial la $ Ox $ $ | a | $ chiar dacă $ a> 0 $ și stânga dacă $ a
- $ y = f \ left (x \ right) + b $ se obține din graficul $ f (x) $ prin deplasarea de la $ Oy $ la $ | b | $ în sus dacă $ b> 0 $ și în jos dacă $ \
- $ y = f (kx) $ este obținut din graficul $ f (x) $ prin contracția la axa $ Oy $ dacă $ k> 1 $ și întinderea dacă $ 0
- $ y = kf (x) $ este obținută din $ f (x) $ prin întinderea $ k $ times de la $ Ox $ dacă $ k> 1 $ și contractarea la $ Ox $ în $ \ frac $ times dacă $ 0
- $ y = f (-x) $ se obține din graficul $ f (x) $ printr-o hartă simetrică în raport cu axa $ Oy $.
- $ y = -f (x) $ este obținut din graficul $ f (x) $ printr-o hartă simetrică față de axa $ Ox $.
- $ y = | f | left (x | right) | $ este obținut din graficul $ f (x) $ după cum urmează: partea de grafic $ f (x) $ situată deasupra axei $ Ox $ rămâne neschimbată și $ Ox $ este afișat simetric în jurul axei $ Oy $.
- $ y = f \ left (| x | \ right) $ se obține din graficul $ f (x) $ după cum urmează: partea graficului $ f (x) $ care se află în dreapta axei $ Oy $ rămâne neschimbată este simetric cu privire la axa $ Oy $, înlocuind partea situată în stânga lui $ Oy $.
Exemplu de cercetare și construcție a unei funcții
Explorați funcția și construiți graficul:
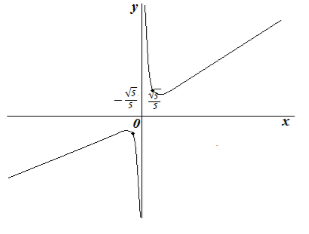
\ [y = \ frac \]- Domeniul de definiție este $ \ left (- \ infty, 0 \ right) (0, \ infty) $. Valoarea intervalului: $ \ stânga (- \ infty, 1-2 \ sqrt \ right] [1 + 2 \ sqrt, \ infty) $
- funcția nu este nici măcar ciudată, neperiodică.
- Nu există puncte de intersecție cu axele de coordonate.
Dacă $ x \ in \ din stânga (- \ infty, 0 \ dreapta) funcția $ este negativ, la $ x \ in \ din stânga (0, \ infty \ dreapta) $ este pozitiv.
Prin metoda intervalului, obținem asta
Funcția crește cu $ x \ în \ left (- \ infty, - \ frac> \ right) \ stânga (\ frac>, \ infty \ right) $ și scade ca $ x \ \ right) \ stânga (0, \ frac> \ dreapta) $
Valoarea maximă a funcției: $ \ left (- \ frac>, 1-2 \ sqrt \ right) $
Minimul funcției: $ \ left (\ frac>, 1 + 2 \ sqrt \ right) $
Prin metoda de intervale obținem că funcția este convexă pentru $ x \ in \ left (0, \ infty \ right) $ și concavă ca $ x \ în \ left (- \ infty, 0 \ right) $